Enterprise Risk Management Formula Book
[this page | pdf | back links]
1. Function definitions
Gamma, incomplete gamma,
beta, incomplete beta, regularised incomplete beta, binomial
2. Series expansions
Exponential, natural
logarithm, binomial, Taylor series
3. Calculus
Integration by parts,
changing order of integration, differentiating an integral
4. Statistical distributions
Probability distribution
terminology, Bayes’ theorem, compound distributions
5. Statistical methods
Sample moments,
parametric inference (with normal underlying distributions), maximum likelihood
estimators, method-of-moments estimators, goodness of fit, linear regression,
generalised linear models, correlations, analysis of variance, Bayesian priors
and posteriors
6. Monte Carlo methods
Creation of normal random
variables, Cholesky decomposition
7. Interest rates and bond pricing
Spot and forward rates, duration,
modified duration, gross redemption yield (yield to maturity), credit spread,
option-adjusted spread, annualisation conventions
8. Financial derivatives
Forward prices,
Black-Scholes formulae
9. Risk measures
Value-at-Risk, tail
Value-at-Risk, expected shortfall, expected worst outcome, tracking error,
drawdown, marginal VaR, incremental VaR, estimating VaR
10. Portfolio optimisation
Mean-variance
optimisation, capital asset pricing model
11. Extreme value theory
Maximum domain of
attraction, Fisher-Tippett theorem, Pickands-Balkema-de Hann theorem,
estimating tail distributions
12. Copulas
Definition, properties, Sklar’s
theorem, example copulas, tail dependence, simulating copulas
13. Miscellaneous
Combining solvency
capital requirements using correlations, credit risk modelling, GARCH modelling,
linear algebra and principal components, central limit theorem, Cornish-Fisher
asymptotic expansion, Euler capital allocation principle, equiprobable outcomes
for a multivariate normal distribution, RAROC and EVA
Appendix A: Probability distributions
Discrete: Binomial
(and Bernoulli), Poisson
Continuous: Normal,
uniform, chi-squared, exponential, F, generalised extreme value (GEV)
(and Frechét, Gumbel and Weibull), generalised Pareto, lognormal, Student’s t
Other: Distributional
mixtures, location and scale adjusted distributions, multivariate
distributions, distributional families
Tables: cumulative
distribution function and quantile function for normal distribution
Note: In this note,
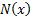 denotes
the standard cumulative normal distribution function,
denotes
the standard cumulative normal distribution function, 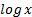 denotes
logarithms to base
denotes
logarithms to base 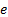 ,
, 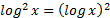 etc.
but if
etc.
but if 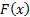 is
a cumulative distribution function then
is
a cumulative distribution function then 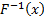 is
the corresponding inverse cumulative distribution function.
is
the corresponding inverse cumulative distribution function.
NAVIGATION LINKS
Contents | Next