Performance Measurement Theory
3. Performance attribution
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next
page
3.1 Portfolios will typically contain several
sectors, in which case, given the same linear approximation as used above, the
total fund and benchmark returns, 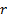 and
and 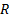 will
be as follows,
will
be as follows, 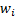 = mean fund
weighting for sector
= mean fund
weighting for sector 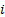 ,
, 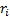 = return for
that individual sector etc,
= return for
that individual sector etc, 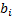 = benchmark
weighting for sector
= benchmark
weighting for sector 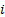 and
and 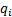 = return
on benchmark for sector
= return
on benchmark for sector 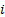 :
:
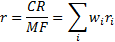
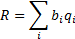
where 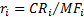 and
and 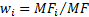
3.2 Their difference is therefore as follows (since
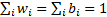 ):
):
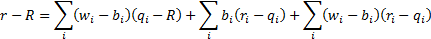
3.3 We can rewrite the relative performance as
follows:
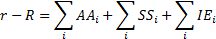
where 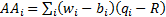 ,
, 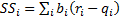 and
and 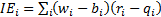 .
.
3.4 The 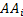 are the
contributions from ‘asset allocation’, the
are the
contributions from ‘asset allocation’, the 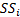 are the
contributions from ‘stock selection’ and the
are the
contributions from ‘stock selection’ and the 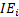 are the
contributions from an ‘interaction effect’. The interaction effect is the
cross-product term that arises from the fact that the value added by stock
selection is based on the amount of assets involved. Typically, the interaction
effect is added into stock selection if you are a ‘top-down’ manager and into
asset allocation if you are a ‘bottom-up’ manager.
are the
contributions from an ‘interaction effect’. The interaction effect is the
cross-product term that arises from the fact that the value added by stock
selection is based on the amount of assets involved. Typically, the interaction
effect is added into stock selection if you are a ‘top-down’ manager and into
asset allocation if you are a ‘bottom-up’ manager.
3.5 The above analysis concentrates on additive
attribution. To make the contributions from asset allocation and stock
selection chain-link they can be restated in a geometric fashion as follows: 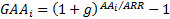 and
and 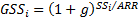 (and a
corresponding
(and a
corresponding 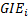 if the
interaction term is kept separate) where
if the
interaction term is kept separate) where 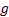 =
geometric relative return at total assets level,
=
geometric relative return at total assets level, 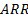 =
additive relative return at total assets level and
=
additive relative return at total assets level and 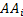 and
and 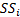 are the
additive asset allocation contribution and additive stock selection
contribution from sector
are the
additive asset allocation contribution and additive stock selection
contribution from sector 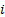 . Or, one can use
natural logarithms using, say,
. Or, one can use
natural logarithms using, say, 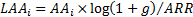 so that
so that 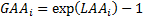 . The total
logarithmic contribution to return from a particular source over several
periods can then be found merely by adding these terms together over.
. The total
logarithmic contribution to return from a particular source over several
periods can then be found merely by adding these terms together over.
3.6 Decomposing returns by ‘factors’ is
conceptually quite similar. However, we also need:
(a) For both fund
and benchmark, the average exposure to each factor involved in the
decomposition, say 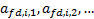 and
and 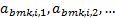
(b) For the benchmark
only, the return a sector would deliver with zero factor exposure, 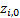 and the extra
return for a unit exposure to each individual factor (for each sector), say:
and the extra
return for a unit exposure to each individual factor (for each sector), say: 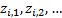 so that
so that 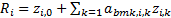 .
.
3.7 The relative return can then be decomposed
into:
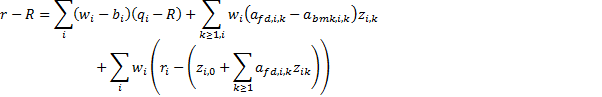
3.8 The first term is the contribution from asset
allocation, the second the component of the stock selection explained by the
various factors, and the third the residual component of stock selection which
is unexplained by the various factors. The second term would normally be shown
decomposed by both sector and factor. The sector analysis described above is a
special case with 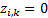 and with more
than one value for
and with more
than one value for 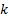 . We would
ideally want to build up the
. We would
ideally want to build up the 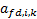 by
calculating the corresponding factor exposures by line of stock and then
aggregating to the sector level. We might also do this for the benchmark as
well or we might use a separate summarised data source.
by
calculating the corresponding factor exposures by line of stock and then
aggregating to the sector level. We might also do this for the benchmark as
well or we might use a separate summarised data source.
3.9 Currency effects can be accommodated within
this framework by including as separate ‘sectors’ any currency hedges away from
the fund’s base position. If the base position is a hedged benchmark then these
would be reverse hedges to reintroduce exposure to that currency. Performance
measurers have developed lots of other ways of taking currency into account,
although many only seem particularly relevant for certain ways in which
currency decisions might be taken vis-à-vis sector or security selection decisions.
NAVIGATION LINKS
Contents | Prev | Next