Nematrian Website Pages on General
Relativity and Gravitation
[this page | pdf | references | back links]
Most people are fascinated by how the universe works. We are
all part of it! And gravity is one of its more obvious manifestations. Gravity
influences our every movement, as well as guiding the motion of planets and
stars.
Mankind’s current understanding of gravity is encapsulated
in Albert Einstein’s General Theory of Relativity. In the limit of weak
gravitational fields and slow motion the geodesic
hypothesis that underlies it seems to imply the same behaviour as
its predecessor, Newtonian Gravity. To the extent that we can measure them, its
predictions regarding deviations from Newtonian theory in stronger
gravitational fields and fast motion seem to match observed behaviour. In
particular it was able to explain an already observed anomaly in the orbit of Mercury
around the Sun. It also predicted that light rays would be bent by their
passage through a gravitational field, a result that was triumphantly
vindicated shortly after the theory was formulated. Quite apart from its
apparent accuracy as a description of how the universe operates, it possesses a
deep mathematical elegance that makes it appealing to those who study it. As Hughston
and Tod (1990) put it, the theory “has that rare quality about it
that excites all of one’s attentions in a physical theory: it has an air of
permanence ... a study worthy of intellectual enquiry by students who, after
coming to understand it, will not in any ordinary sense have any practical used
for it. It is a work of art.”
Of course, this is not to say that there are not some
challenges with the theory. Physicists generally believe that it cannot be
effectively melded together with that other great physical theory of our time,
quantum mechanics, in relation to what happens at the event horizons of the
so-called ‘black holes’ that appear to be predicted by General Relativity. This
has led to the search for some more effective synthesis of the two theories (or
their replacement), which loosely goes under the name ‘quantum gravity’ or,
more prosaically, the ‘Theory of Everything’. This is the first of the five
major unsolved problems of modern physics, according to Smolin.
Many physicists believe that a leading contender to achieve this synthesis is
‘string theory’.
Another potential challenge that General Relativity faces is
that it is difficult to reconcile the observed behaviour of some galaxy systems
with the masses of these systems that we appear to be able to see within them.
The usual way of resolving these latter observational
challenges is to postulate the existence of so-called ‘dark matter’, which is
some as yet unknown form of matter that provides the right additional gravitational
pull within these types of galaxy systems to explain the otherwise anomalous
observations. An alternative approach, called Modified Newtonian Dynamics
(MOND), is advanced by some commentators. It assumes that there is some
breakdown in the way in which Newtonian dynamics works when gravitation
acceleration is less than a certain (quite small) value. MOND is
phenomenologically quite successful, in the sense that it takes only one relatively
straightforward modification to Newtonian gravity to explain a surprisingly
large number of these apparently anomalous observations. However, no-one has
yet come up with any convincing theoretical reason for such a modification, so
it has generally not found favour with theoretical physicists.
Malcolm Kemp’s book on Market Consistency
notes an analogy between how the ‘axioms’ underlying Market Consistency operate
and how Einstein’s General Theory of Relativity. In this book the author,
amongst other things, argues that the ‘interesting’ (and most challenging)
aspects of Market Consistency arise when some element of the axioms underlying
it break down. In General Relativity, the Riemann tensor measures the extent to
which the curved space-time equivalent of differentiation does not satisfy the
axiom of commutativity, i.e. does not adhere to 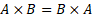 .
It is thus also intimately bound up with the extent to which space-time is
curved. The Einstein tensor, which derives from the Riemann tensor, is proportional
to the amount of matter or energy present. So in a sense we can view the force
of gravity, and hence the ‘interesting’ aspects of General Relativity (as far
as we are concerned), as also being driven by the extent to which a particular ‘axiom’
(here an axiom of commutativity) does not in fact apply in the real world.
.
It is thus also intimately bound up with the extent to which space-time is
curved. The Einstein tensor, which derives from the Riemann tensor, is proportional
to the amount of matter or energy present. So in a sense we can view the force
of gravity, and hence the ‘interesting’ aspects of General Relativity (as far
as we are concerned), as also being driven by the extent to which a particular ‘axiom’
(here an axiom of commutativity) does not in fact apply in the real world.
References
Hughston,
L.P. and Tod, K.P. (1990). An Introduction to General Relativity.
Cambridge University Press
Smolin, L.
(2006). The Trouble with Physics: The Rise of String Theory, the
Fall of a Science and What Comes Next. Allen Lane (an imprint of Penguin
Books)