The geodesic hypothesis
[this page | pdf | references | back links]
The normal way in which textbooks introduce Einstein’s
Theory of General Relativity is via the geodesic hypothesis. This is the
hypothesis that small ‘freely-falling’ bodies move along geodesic trajectories
(i.e. the curved space equivalent of straight lines), see e.g. Hughston
and Tod (1990). This hypothesis is usually itself derived from the equivalence
principle, i.e. the assumption that it is impossible to differentiate in
physical experiments confined to infinitesimally small regions of space time
between two different inertial frames of reference. Indeed, Einstein himself
articulated the principle of local equivalence in 1911:
“We arrive at a very
satisfactory interpretation of this law of experience, if we assume that the
systems K and K’ are physically exactly equivalent, that is, if we assume that
we may just as well regard the system K as being in a space free from
gravitational fields, if we then regard K as uniformly accelerated. This
assumption of exact physical equivalence makes it impossible for us to speak of
the absolute acceleration of the system of reference, just as the usual theory
of relativity forbids us to talk of the absolute velocity of a system; and it
makes the equal falling of all bodies in a gravitational field seem a matter of
course.”
A cornerstone of the argument that many people use to
postulate the existence of ‘dark matter’ is that the trajectories that objects
(including light rays) take in certain large astronomical systems appear to
deviate from the geodesic hypothesis if one merely takes account of the amount
of visible matter that appears to be within them. Arguably there are only two
broad ways in which we can explain deviation from Newtonian trajectories of
slowly moving objects in weak gravitational fields derived from a certain
amount of visible matter. These are if there is some additional unaccounted for
‘dark’ matter (which alters the magnitude of the gravitational field in the
observed manner) or if there is a breakdown in the geodesic hypothesis.
The argument may be developed as follows. Consider why it is
that we equate the constant of proportionality,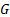 
,
in Einstein’s field equations with the Newtonian gravitational constant.
Typically the linkage is derived along the following lines, see e.g. Hughston
and Tod (1980):
(a) In weak
gravitational fields we assume locally that we can find a coordinate system
that is in a suitable sense approximately Cartesian, so that the metric tensor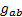 
in this coordinate
system is equal to the Minkowski (flat-space) metric plus a smaller term, say,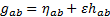 
, where 
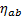is the flat-space
metric (so ‘weak’ here means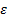 
is small). We also
assume that with respect to this coordinate system we have for all functions,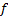 
,
of interest for 
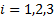(here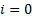 
corresponds
to the time dimension):
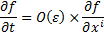
(b) The ‘slow-motion
approximation’ then leads us to conclude that for a slowly moving particle the
geodesic equations reduce to the following, where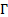 
are the Christoffel
symbols:
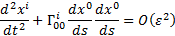
(c) But (a) implies
that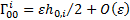 
, using Hughston and
Tod’s notation, so the geodesic equation reduces to:
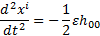
This equation equates to
Newtonian gravitational theory only if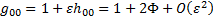 
where 
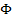is the Newtonian
gravitational potential.
Hughston
and Tod (1980) note that “any theory of gravitation that
incorporates the geodesic hypothesis [i.e. that particles travel along
geodesics] must make [this identification], so that this is not a unique characteristic
of general relativity”. Indeed, any theory of gravitation (including General
Relativity) that adheres to the geodesic hypothesis will be approximately
Newtonian for objects satisfying the slow motion approximation and moving in
weak gravitational fields.
References
Hughston,
L.P. and Tod, K.P. (1990). An Introduction to General Relativity.
Cambridge University Press