Tail Fitting of a Normal Distribution
[this page | pdf | back links]
One approach for fitting the tail of a distribution is to
select an appropriate distributional family and then to select the parameters
characterising the distribution in a manner that provides the best fit of the
observed (cumulative) distribution function and/or quantile-quantile plot in
the relevant tail.
Suppose that the observations are 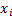 for
for
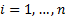 .
When ordered these are say
.
When ordered these are say 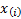 .
Weights given to each observation in the curve fitting process are
.
Weights given to each observation in the curve fitting process are 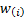 .
Typically we might expect the
.
Typically we might expect the 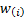 to
be non-zero (and then typically constant) only for
to
be non-zero (and then typically constant) only for 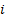 sufficiently
small, or for
sufficiently
small, or for 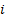 sufficiently large, although
this is not strictly necessary.
sufficiently large, although
this is not strictly necessary.
A common way of carrying out curve fitting is least squares,
so a natural way of implementing this approach to fit a (univariate) Normal
distribution to the data might be:
Any Normal distribution is characterised by a mean, 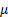 , and standard
deviation,
, and standard
deviation, 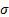 . We might therefore derive,
. We might therefore derive, 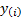 ,
the expected value for the observation
,
the expected value for the observation 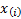 ,
using the following formula:
,
using the following formula:
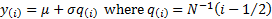
[Note, the expected value of 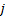 ’th quantile of
a Normal distribution is not precisely
’th quantile of
a Normal distribution is not precisely 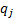 as
defined above because the pdf is not flat, see e.g. Expected Worst
Loss Analysis]
as
defined above because the pdf is not flat, see e.g. Expected Worst
Loss Analysis]
We would then identify estimates of the mean, 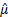 ,
and standard deviation,
,
and standard deviation, 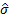 ,
that together minimise the following least squares computation:
,
that together minimise the following least squares computation:
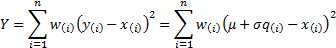
This is minimised when 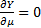 and
and
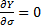 ,
i.e. for the values of
,
i.e. for the values of 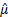 and
and
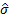 where:
where:
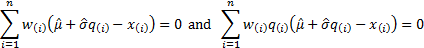
If 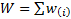 ,
,
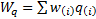 ,
,
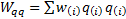 ,
,
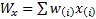 and
and
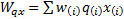 then
these equations simplify to:
then
these equations simplify to:
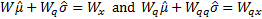
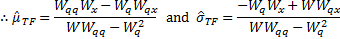
Whilst this type of approach is primarily designed to be
used merely in the tail of the distribution (i.e. with 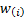 non-zero,
perhaps constant, only for
non-zero,
perhaps constant, only for 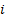 suitably small or, for the other
tail, only for
suitably small or, for the other
tail, only for 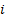 suitably close to
suitably close to 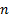 ), we can also
consider what answer this approach would give if it were applied to the entire
distributional form, e.g. using
), we can also
consider what answer this approach would give if it were applied to the entire
distributional form, e.g. using 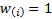 for
all
for
all 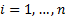 . As the
. As the 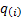 are
symmetric around 0.5, we have
are
symmetric around 0.5, we have 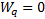 so
so
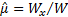 ,
i.e.
,
i.e. 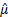 is
then the usual maximum likelihood estimator
is
then the usual maximum likelihood estimator 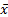 .
By, say, carrying out a simulation exercise we can also confirm that
.
By, say, carrying out a simulation exercise we can also confirm that 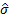 is
also typically close to the relevant maximum likelihood estimator if
is
also typically close to the relevant maximum likelihood estimator if 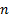 is not very
small.
is not very
small.