The normal distribution
[this page | pdf | back links]
The normal distribution is a continuous probability
distribution that has a bell-shaped probability density function:
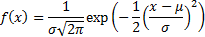
It is usually considered to be the most prominent
probability distribution in statistics partly because it arises in a very large
number of contexts as a result of the central limit theorem and partly because
it is relatively tractable analytically.
The normal distribution is also called the Gaussian
distribution. The unit normal (or standard normal) distribution
is 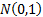 .
.
Characteristics of the normal distribution are set out
below:
![[SmartChart]](I/NormalDistribution_files/image003.gif)
![[SmartChart]](I/NormalDistribution_files/image004.gif)
![[SmartChart]](I/NormalDistribution_files/image005.gif)
|
Distribution name
|
Normal
distribution
|
|
Common notation
|
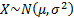
|
|
Parameters
|
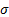 = scale
parameter ( = scale
parameter (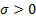 ) )
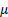 =
location parameter =
location parameter
|
|
Domain
|
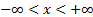
|
|
Probability density
function
|
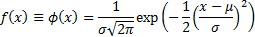
|
|
Cumulative distribution
function
|
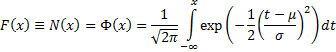
|
|
Mean
|
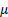
|
|
Variance
|
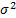
|
|
Skewness
|
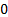
|
|
(Excess) kurtosis
|
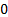
|
|
Characteristic function
|
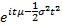
|
|
Other comments
|
The inverse unit normal distribution function (i.e. its
quantile function) is commonly written 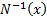 (also
in some texts (also
in some texts 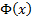 and
the unit normal density function is commonly written and
the unit normal density function is commonly written 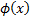 . .
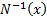 is
also called the probit function. is
also called the probit function.
The error function
distribution is 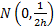 ,
where ,
where 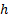 is now an inverse scale
parameter is now an inverse scale
parameter 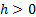 . .
The median and mode of a normal distribution are 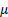 . .
The truncated first moments of 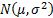 are: are:
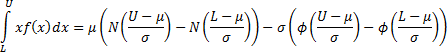
where 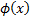 and and
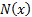 are
the pdf and cdf of the unit normal distribution respectively. are
the pdf and cdf of the unit normal distribution respectively.
The mean excess function of a standard normal distribution
is thus
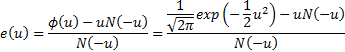
The central moments of the normal distribution are:
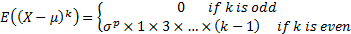
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “normal”. For
details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next