FFT
[this page | pdf]
Function Description
Returns the fast Fourier transform (‘FFT’) (if CarryOutForwardTransform
is true) or the inverse FFT (if CarryOutForwardTransform is false) of an
array of 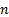 complex numbers (i.e. input array has
complex numbers (i.e. input array has 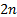 term, the real part
followed by the imaginary part), where
term, the real part
followed by the imaginary part), where 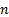 must
be an integral power of two.
must
be an integral power of two.
If the input to the FFT is 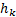 (each
(each
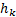 is a
complex number) where
is a
complex number) where 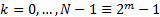 then
the output (of the forward transform) is another array of
then
the output (of the forward transform) is another array of 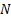 complex numbers as
follows:
complex numbers as
follows:
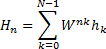
where 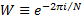 . When
inverting, a constant multiplier is applied to all terms to ensure that the
result of applying the transform to the output of the forward transform and
then applying the transform returns the original series.
. When
inverting, a constant multiplier is applied to all terms to ensure that the
result of applying the transform to the output of the forward transform and
then applying the transform returns the original series.
The FFT calculates the 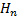 using
using
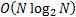 rather
than the
rather
than the 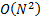 that
might appear to be needed given the above formula. This involves a very large
speed up for large data analyses, e.g. analysing large pictures or other datasets.
that
might appear to be needed given the above formula. This involves a very large
speed up for large data analyses, e.g. analysing large pictures or other datasets.
Some writers use 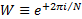 , e.g.
Press et
al. (2007), and some writers multiply the expression with constants, e.g.
, e.g.
Press et
al. (2007), and some writers multiply the expression with constants, e.g. 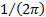 . The
use of
. The
use of 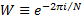 means
that the end result is compatible with output from the Microsoft Excel Data
Analysis Toolpack.
means
that the end result is compatible with output from the Microsoft Excel Data
Analysis Toolpack.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other General functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement