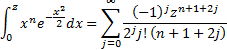Integration of Piecewise Polynomials
against a Gaussian probability density function
[this page | pdf | references | back links]
In a number of financial contexts it can be important to
calculate the following integral:
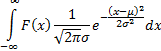
For example, this integral is relevant to calculating
moments of a fat-tailed distribution, i.e. one whose quantile-quantile plot
versus the Normal distribution, 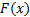 ,
is not unity. The faster
,
is not unity. The faster 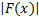 increases
as
increases
as 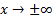 the
greater is the impact of fat-tailed behaviour, i.e. deviations from a density
function of the form
the
greater is the impact of fat-tailed behaviour, i.e. deviations from a density
function of the form 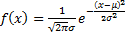 .
Thus risk measures such as expected shortfall (effectively a first moment
computation, in which the leading element of
.
Thus risk measures such as expected shortfall (effectively a first moment
computation, in which the leading element of 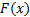 is
of order
is
of order 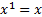 )
are more sensitive to fat-tailed effects than Value-at-Risk risk measures
(effectively a zero moment computation, in which the leading element of
)
are more sensitive to fat-tailed effects than Value-at-Risk risk measures
(effectively a zero moment computation, in which the leading element of 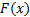 is
of order
is
of order 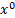 ).
).
This integral can also appear in derivative pricing
analysis, if payoff is being approximated by a piecewise polynomial function
and the movement of the underlying is of a certain type (but see Valuing
polynomial payoffs in a Black Scholes World, which suggests that some
modification may be needed to cater for exponentials arising when converting
the partial differential equation arising under a Gauss-Weiner process to one
with ‘standard’ parabolic form).
Hence, it becomes helpful to be able to calculate the
following integral rapidly:
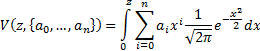
If 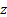 is
large then we note that:
is
large then we note that:
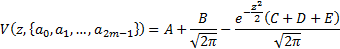
Where
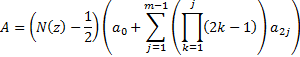
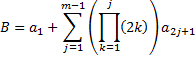
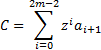
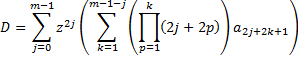
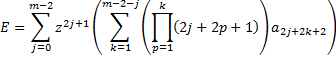
If 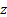 is
small then for higher order coefficients the above computation runs into
machine rounding problems. It is then better to use a Taylor series expansion,
bearing in mind that:
is
small then for higher order coefficients the above computation runs into
machine rounding problems. It is then better to use a Taylor series expansion,
bearing in mind that:
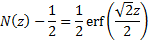
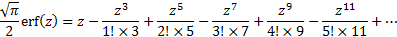
Hence (if 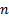 is
integral and
is
integral and 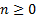 )
we have:
)
we have: