High resolution extended image near field
optics
3. Exact radiating solutions to Maxwell’s
equations in a vacuum
[this page | pdf | references | back links]
Copyright (c) Malcolm
Kemp 2010
Return
to Abstract and Contents
Next
page
The explanation of the unusual properties of the idealised
optical layout described in Section 2 lies in the
behaviour of certain types of exact solutions of Maxwell’s equations in the
presence of idealised plane mirrors.
Before exploring these further, let us first the nature of
radiating solutions to Maxwell’s equations in a vacuum. These can be
written as superpositions of (potentially infinitely many) outwardly and
inwardly radiating electric and magnetic dipoles.
Born & Wolf (1980) describe the behaviour of a single outwardly
radiating electric dipole, characterised by source location 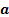 ,
a unit vector,
,
a unit vector, 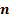 ,
describing the direction in which the dipole is pointing, and an electric
polarization vector
,
describing the direction in which the dipole is pointing, and an electric
polarization vector 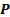 whose
value at point
whose
value at point 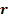 and
at time
and
at time 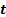 is
given by
is
given by 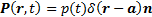 ,
where
,
where 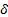 is the Dirac function and
is the Dirac function and 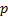 is a function
of time. The full (i.e. exact) solution to Maxwell’s equations (in a vacuum)
for such a dipole then has the following form, where
is a function
of time. The full (i.e. exact) solution to Maxwell’s equations (in a vacuum)
for such a dipole then has the following form, where 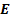 ,
,
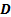 ,
,
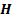 and
and
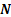 are
the electric field, electric displacement, magnetic and magnetic induction
vectors respectively:
are
the electric field, electric displacement, magnetic and magnetic induction
vectors respectively:
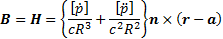
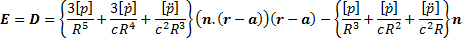
Here 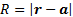 and
and
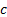 is
the speed of light. Square brackets denote retarded values, i.e.
is
the speed of light. Square brackets denote retarded values, i.e. 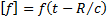 .
.
The form of this solution is slightly easier to visualise in
spherical polar coordinates 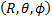 taking
the origin as the source location,
taking
the origin as the source location, 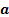 ,
,
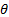 as
the angle between
as
the angle between 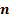 and
and
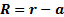 and
and
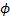 as
the angle that the projection of
as
the angle that the projection of 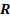 onto
the plane perpendicular to
onto
the plane perpendicular to 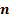 makes
with a constant vector perpendicular to
makes
with a constant vector perpendicular to 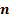 .
If
.
If 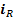 ,
,
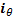 and
and
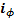 are
unit vectors in the direction of increasing
are
unit vectors in the direction of increasing 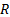 ,
,
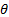 and
and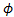 respectively
then the outwardly radiating electric dipole has the form
respectively
then the outwardly radiating electric dipole has the form 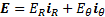 and
and
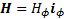 where:
where:
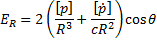
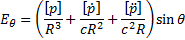
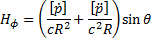
The form of the inwardly radiating electric
dipole, i.e. the time reversed solution, can be found by replacing 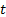 by
by 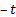 and
and 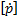 by
by
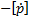 (since
(since
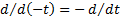 )
and by placing a negative sign in front of the corresponding expressions for
)
and by placing a negative sign in front of the corresponding expressions for 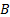 and
and 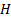 (since
(since 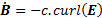 ).
).
The corresponding outwardly and inwardly radiating magnetic
dipoles have 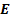 replaced
by
replaced
by 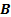 and
and
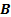 replaced
by
replaced
by 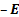 ,
given the symmetric nature of Maxwell’s equations in a vacuum. For reasons that
will become obvious later on, we will concentrate on these latter types of
dipoles in the remainder of this analysis.
,
given the symmetric nature of Maxwell’s equations in a vacuum. For reasons that
will become obvious later on, we will concentrate on these latter types of
dipoles in the remainder of this analysis.
We can further decompose each of these dipoles into
superpositions of sinusoidally time-varying dipoles all with the same origin,
using Fourier analysis. These will be the types of dipoles that we will
concentrate on in the remainder of this analysis. For magnetic dipoles
with 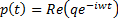 ,
,
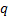 and
and
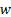 constant,
these have the following form (where
constant,
these have the following form (where 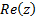 is
the real part of the complex number
is
the real part of the complex number 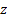 and
and 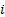 is the square
root of
is the square
root of 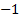 ):
):
Outwardly radiating (magnetic) dipoles
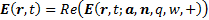
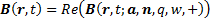
Inwardly radiating (magnetic) dipoles
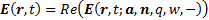
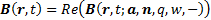
where
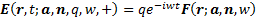
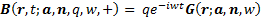
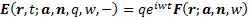
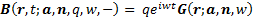
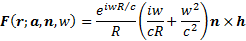
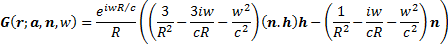
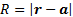
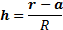
NAVIGATION LINKS
Contents | Prev | Next