High resolution extended image near field
optics
1. Introduction and Conclusions
[this page | pdf | references | back links]
Copyright (c) Malcolm
Kemp 2010
Return
to Abstract and Contents
Next
page
How practical it is to achieve arbitrarily high resolution
with a microscope, telescope or photolithographic device?
In days gone by, this topic would have had a clear answer.
The wave-like nature of light places a limit on the effective resolving power
of conventionally formulated (i.e. ‘far field’) devices. This limit is given by
the well-known Rayleigh’s equation, which states that the minimum distance able
to be resolved by such a microscope or a photolithographic device, 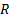 , is set by:
, is set by:
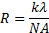
In this formula, 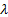 is the wavelength of the light
used,
is the wavelength of the light
used, 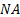 is the numerical aperture of
the device and
is the numerical aperture of
the device and 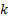 is a constant that depends on
the image formation technique used and (for microscopy or photolithography) the
specific resist being used in the device. A similar equation, involving the
aperture size and wavelength limits the angular resolving power of a (conventional)
telescope.
is a constant that depends on
the image formation technique used and (for microscopy or photolithography) the
specific resist being used in the device. A similar equation, involving the
aperture size and wavelength limits the angular resolving power of a (conventional)
telescope.
However, given the huge technological and economic benefits
accruing from squeezing ever finer circuitry onto microchips, cunning
researchers have squeezed down the value of 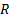 using
a variety of techniques. Some have involved improving
using
a variety of techniques. Some have involved improving 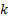 using
‘unconventional’ designs, some have involved shortening the wavelength of light
being used, and some have involved lenses with enhanced numerical apertures,
see e.g. Ito
and Okazaki (2000) for further details.
using
‘unconventional’ designs, some have involved shortening the wavelength of light
being used, and some have involved lenses with enhanced numerical apertures,
see e.g. Ito
and Okazaki (2000) for further details.
Perhaps the most extreme example of an ‘unconventional’
design is the scanning near field optical microscope (‘SNOM’). This works in a
manner similar to a scanning tunnelling electron microscope, in that the
microscope is placed a fraction of a wavelength away from the object being imaged.
The Rayleigh equation no then longer applies and arbitrarily accurate
resolution is in theory possible (even to the level of individual molecules or,
with scanning tunnelling electron microscopes, individual atoms).
SNOM’s operate by shining light through a very small hole
which is placed very close to the object being imaged or projected onto. In
principle, SNOM’s have arbitrarily high resolving power, since in theory their
accuracy is limited only by the size of the hole through which the light is
shone. In practice, however, their resolution is limited because of the finite
skin depth of real metals, or in other words because idealised metals with
infinitely high (complex) refractive indices do not actually exist. This places
a lower limit on the effective hole size that it is possible to achieve in
practice (although it is possible circumvent this limit to some extent by
arranging for the light source to be a single molecule).
It is possible to use the same approach in reverse for
lithography, although Ito and
Okazaki (2000) express the view that “although such approaches are useful
for producing individual nano-structures for the investigation of
nanometre-scale devices, the throughput is likely to always remain
impracticably low for commercial application”.
What is less clear is whether near field optical lithography
(or microscopy) necessarily has to operate a point at a time, and therefore
whether the assumed commercial barrier indicated by Ito and
Okazaki (2000) is correct. We show that this assumption is probably false
and that a resolving power similar to that achievable by existing SNOM designs
should in principle be achievable by a near field device that creates an
extended spatial image ‘all at once’. We shall also describe how in principle
this approach might be used to create a telescope that also circumvents the
Rayleigh resolution limit, despite how far away any practical object being
viewed will be from the viewing telescope.
Whether these ideas will ever prove practical and/or commercial
is more difficult to say – they were originally set out in a patent application
in 2001, see Kemp
(2001) and have not developed further since then. Other arguably more
commercial techniques have since been developed that also ‘stretch the
envelope’ of what is possible with high resolution optical lithography.
However, continued improvement in resolving power is one of the key drivers
needed to maintain Moore’s law and the microchip revolution we are all
benefiting from. Perhaps, one day, the ideas set out in these pages will
therefore prove useful and fruitful, if other methods of stretching the
envelope run out of steam.
NAVIGATION LINKS
Contents | Prev | Next