The generalised Pareto distribution
[this page | pdf | references | back links]
The generalised Pareto distribution (generalized Pareto
distribution) arises in Extreme Value Theory
(EVT). If the relevant regularity conditions are satisfied then the tail of a
distribution (above some suitably high threshold), i.e. the distribution of
‘threshold exceedances’, tends to a generalized Pareto distribution.
Care is needed with EVT because what we are in effect doing
with it is to extrapolate into the tail of the distribution. Extrapolation is
an intrinsically imprecise and subjective mathematical activity. We can in
effect view the regularity conditions that need to be satisfied if EVT applies
as corresponding to requiring that this extrapolation is done in a particular
manner.
![[SmartChart]](I/GeneralisedParetoDistribution_files/image001.gif)
![[SmartChart]](I/GeneralisedParetoDistribution_files/image002.gif)
![[SmartChart]](I/GeneralisedParetoDistribution_files/image003.gif)
|
Distribution name
|
Generalised
Pareto distribution (GPD)
|
|
Common notation
|
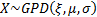
|
|
Parameters
|
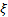 =
shape parameter =
shape parameter
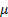 =
location parameter =
location parameter
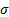 =
scale parameter ( =
scale parameter (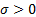 ) )
|
|
Domain
|
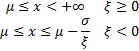
|
|
Probability density
function
|
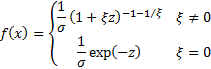
where
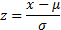
|
|
Cumulative distribution
function
|
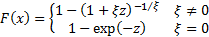
|
|
Mean
|
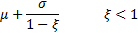
|
|
Variance
|
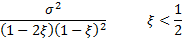
|
|
Skewness
|
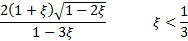
|
|
(Excess) kurtosis
|
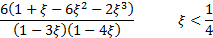
|
|
Other comments
|
If 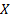 is uniformly
distributed, is uniformly
distributed, 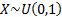 then the
variable then the
variable 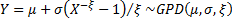 . .
The mean excess function for a GPD, i.e. 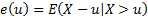 takes a
particularly simple form which is linear in takes a
particularly simple form which is linear in 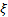 ,
i.e. ,
i.e.
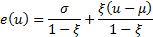
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “generalised
pareto”. For details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next