The Gaussian copula
[this page | pdf | back links]
The Gaussian copula is the copula that underlies the
multivariate normal distribution.
|
Copula name
|
Gaussian copula
|
|
Common notation
|
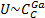
|
|
Parameters
|
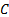 , a
non-negative definite , a
non-negative definite 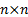 matrix, i.e. a matrix that
can correspond to a correlation matrix matrix, i.e. a matrix that
can correspond to a correlation matrix
|
|
Domain
|

|
|
Copula
|
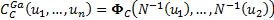
where 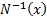 is
the inverse normal
function and is
the inverse normal
function and 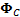 is
the cumulative distribution function of the multivariate normal distribution
defined by a covariance matrix equal to is
the cumulative distribution function of the multivariate normal distribution
defined by a covariance matrix equal to 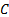
|
|
Kendall’s rank
correlation coefficient (for bivariate case), 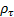
|
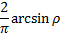
Where 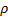 is the correlation
coefficient between the two variables is the correlation
coefficient between the two variables
|
|
Coefficient of upper
tail dependence, 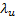
|
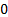 (unless the
correlation matrix exhibits perfect positive or negative dependence) (unless the
correlation matrix exhibits perfect positive or negative dependence)
|
|
Coefficient of lower tail
dependence, 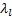
|
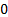 (unless the
correlation matrix exhibits perfect positive or negative dependence) (unless the
correlation matrix exhibits perfect positive or negative dependence)
|
|
Other comments
|
The Spearman rank
correlation coefficient is given by:
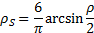
where 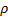 is the (normal) correlation coefficient
between the two variables. is the (normal) correlation coefficient
between the two variables.
If 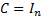 (the (the
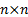 identity
matrix) then we obtain the independence copula. identity
matrix) then we obtain the independence copula.
|
Nematrian web functions
Functions relating to the above distribution in the two
dimensional case may be accessed via the Nematrian
web function library by using a DistributionName of “Gaussian Copula
(2d)”. For details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next