The generalised extreme value
distribution
[this page | pdf | back links]
The generalised extreme value (or generalized extreme value)
distribution characterises the behaviour of ‘block maxima’ under certain
(somewhat restrictive) regularity conditions. See also Nematrian’s webpages
about Extreme Value
Theory (EVT).
![[SmartChart]](I/GEVDistribution_files/image001.gif)
![[SmartChart]](I/GEVDistribution_files/image002.gif)
![[SmartChart]](I/GEVDistribution_files/image003.gif)
|
Distribution name
|
Generalised
extreme value (GEV) distribution (for maxima)
|
|
Common notation
|
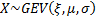
|
|
Parameters
|
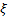 = shape
parameter = shape
parameter
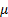 = location
parameter = location
parameter
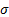 = scale
parameter = scale
parameter
|
|
Domain
|
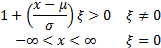
|
|
Probability density
function
|
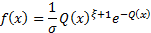
where
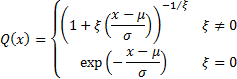
|
|
Cumulative distribution
function
|
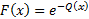
|
|
Mean
|
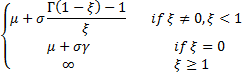
where 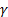 is Euler’s constant, i.e. is Euler’s constant, i.e. 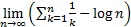
|
|
Variance
|
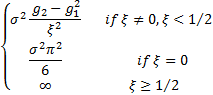
Where 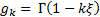
|
|
Skewness
|
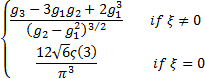
where 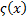 is
the Riemann zeta function, i.e. is
the Riemann zeta function, i.e. 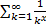 . .
|
|
(Excess) kurtosis
|
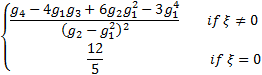
|
|
Other comments
|
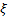 defines the tail behaviour
of the distribution. The sub-families defined by defines the tail behaviour
of the distribution. The sub-families defined by 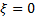 (Type I), (Type I),
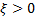 (Type
II) and (Type
II) and 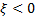 (Type III) correspond to the
Gumbel, Frechét and Weibull families
respectively. (Type III) correspond to the
Gumbel, Frechét and Weibull families
respectively.
An important special case when analysing threshold
exceedances involves 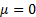 (and normally (and normally 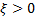 ) and this
special case may be referred to as ) and this
special case may be referred to as 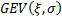 . .
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “gev”. For
details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next