Extreme Events – Specimen Question
A.2.3(a) – Answer/Hints
[this page | pdf | references | back links]
Return
to Question
Q. Recalculate the mean,
standard deviation, skew and kurtosis weighting the data as above. Are they
still suggestive of fat-tailed behaviour?
The proposed exponential weighting approach gives the
following weights to the observations:
|
Period
|
Weight
|
A (logged return)
|
|
1
|
0.2679434
|
-0.2890163
|
|
2
|
0.2871746
|
0.0009995
|
|
3
|
0.3077861
|
0.2167230
|
|
4
|
0.3298770
|
0.0760347
|
|
5
|
0.3535534
|
-0.0140989
|
|
6
|
0.3789291
|
0.0049875
|
|
7
|
0.4061262
|
-0.0060181
|
|
8
|
0.4352753
|
0.0099503
|
|
9
|
0.4665165
|
0.0704585
|
|
10
|
0.5
|
-0.1278334
|
|
11
|
0.5358867
|
0.0069756
|
|
12
|
0.5743492
|
0.0079682
|
|
13
|
0.6155722
|
-0.0387408
|
|
14
|
0.6597540
|
0.0276152
|
|
15
|
0.7071068
|
-0.0439519
|
|
16
|
0.7578583
|
-0.0120726
|
|
17
|
0.8122524
|
-0.0725707
|
|
18
|
0.8705506
|
0.0629748
|
|
19
|
0.9330330
|
0.0353671
|
|
20
|
1
|
0.0178399
|
The ordinary mean of a set of numbers is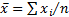 
, where
the 
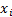are the
observations and there are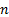 
of them.
The weighted mean, if each observation is given a weight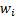 
is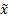 
, say,
where:
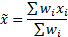
We see immediately that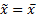 
if the
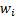observations are given equal weight, i.e. if all the are
equal.
It is relatively simple to calculate this statistic from the
above data using Microsoft Excel (or using the Nematrian web function MnWeightedMean), giving
an answer of -0.0007543
However, identifying exactly how to calculate the
corresponding weighted standard deviation, skew and kurtosis is less simple,
particularly if our focus is on small samples.
For ‘population’ statistics, i.e. those applicable if we
have large observation sets, the calculations involved appear to be relatively
unambiguous, see WeightedMomentsAndCumulants
However, for ‘sample’ statistics, there appear to be
differences in opinion in how, precisely, to adjust ‘population’ statistics to
allow for the different degrees of freedom that are present. Given this
apparent disagreement between commentators, the Nematrian website provides web
functions for calculating the weighted population mean, standard deviation,
skew and excess (excess) kurtosis, but only corresponding weighted sample mean,
standard deviation and skew (i.e. not yet weighted sample excess kurtosis). Rimoldini (2013)
proposes some formulae for these statistics, which appear to match the Nematrian
formulae.
Formulae used by the Nematrian website can be accessed using
the following web functions: MnWeightedPopulationStdev,
MnWeightedPopulationSkew,
MnWeightedPopulationKurt,
MnWeightedStdev and
MnWeightedSkew and
give the following results for the above data:
|
Statistic
|
Unweighted (population)
|
Unweighted (sample)
|
Weighted (population)
|
Weighted (sample)
|
|
Mean
|
-0.0033204
|
-0.0033204
|
-0.0007543
|
-0.0007543
|
|
Standard deviation
|
0.0930001
|
0.0954161
|
0.0741301
|
0.0763675
|
|
Skew
|
-0.791166
|
-0.9253403
|
-0.8903571
|
-0.9761716
|
|
(Excess) kurtosis
|
2.6500366
|
4.6238918
|
5.0848899
|
N/A
|
These statistics are still strongly suggestive of fat-tailed
behaviour.
NAVIGATION LINKS
Contents | Prev | Next | Question