A potential way in which the Central
Limit Theorem (CLT) can break down via combinations of lots of independent
gamma distributed random variables
[this page | pdf | references | back links]
The Gamma distribution has the the ‘summation’ property that
if 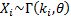 for
for
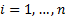 and
the
and
the 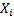 are
independent then
are
independent then 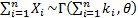 .
.
So, suppose 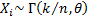 .
Then
.
Then 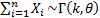 . Thus we appear to be
combining more and more (independent) random variables each of which has
smaller and smaller mean,
. Thus we appear to be
combining more and more (independent) random variables each of which has
smaller and smaller mean, 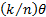 ,
and variance,
,
and variance, 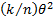 ,
so we might expect the Central Limit Theorem (CLT) to apply.
,
so we might expect the Central Limit Theorem (CLT) to apply.
In fact, for the CLT to apply we need somewhat more onerous
regularity conditions to be satisfied, including a focus on 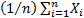 and
(usually) that the distributions of the
and
(usually) that the distributions of the 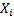 do
not change as
do
not change as 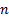 changes (as well as being
of finite variance). The above example does not satisfy these amplified
regularity conditions because as
changes (as well as being
of finite variance). The above example does not satisfy these amplified
regularity conditions because as 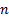 changes the distribution
of each
changes the distribution
of each 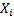 changes.
Although the means (and variances) get smaller and smaller (which you would
have thought would help with satisfying the CLT), each individual
changes.
Although the means (and variances) get smaller and smaller (which you would
have thought would help with satisfying the CLT), each individual 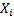 becomes
more and more skewed and has a greater and greater (excess) kurtosis, see e.g.
the Nematrian webpage on the Gamma distribution.
becomes
more and more skewed and has a greater and greater (excess) kurtosis, see e.g.
the Nematrian webpage on the Gamma distribution.