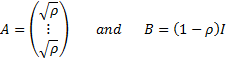Showing that a Gaussian copula is not in
general an Archimdean copula
[this page | pdf | back links]
An 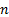 -dimensional Archimedean
copula is one that can
be represented by:
-dimensional Archimedean
copula is one that can
be represented by:
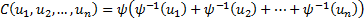
One way of showing that the Gaussian copula is not in
general an Archimedean copula is to consider a three dimensional Gaussian
copula. Its copula density (for a correlation matrix 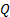 )
can be written as:
)
can be written as:
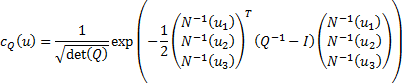
In general, 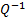 will have 3
different off-diagonal elements, derived from the three different correlations
between
will have 3
different off-diagonal elements, derived from the three different correlations
between 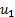 and
and 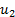 , between
, between 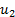 and
and 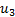 and between
and between 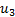 and
and 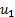 respectively.
Thus the form of the copula density if
respectively.
Thus the form of the copula density if 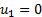 expressed as
a function of the remaining two components of
expressed as
a function of the remaining two components of 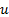 ,
i.e. here
,
i.e. here 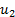 and
and 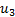 , will differ
from its form if
, will differ
from its form if 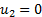 expressed as
a function of
expressed as
a function of 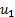 and
and 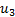 etc.
However, to be Archimedean, the copula needs to be indifferent between the
components of
etc.
However, to be Archimedean, the copula needs to be indifferent between the
components of 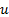 .
.
For 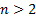 , the
Gaussian copula has too many free parameters to be Archimedean.
, the
Gaussian copula has too many free parameters to be Archimedean.
Conversely, if returns are multivariate normal and have an
exchangeable copula then the returns can be characterised by a factor structure
involving a single factor.
A set of 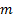 random
variables,
random
variables, 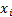 (
(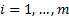 )
is said to possess a factor structure if their covariance matrix,
)
is said to possess a factor structure if their covariance matrix, 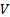 ,
is of the form
,
is of the form 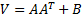 where
where 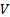 is
an
is
an 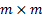 matrix,
matrix, 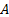 is
an
is
an 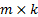 matrix (and
there are
matrix (and
there are 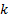 factors) and
factors) and
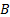 is a
diagonal matrix. Suppose the variance of each
is a
diagonal matrix. Suppose the variance of each 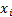 is
is 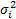 and we
define
and we
define 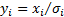 . Then
. Then 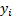 have unit
variance and their covariance (now also correlation) matrix also has the form
have unit
variance and their covariance (now also correlation) matrix also has the form 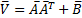 . The copulas
describing the
. The copulas
describing the 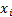 and
and 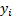 are the
same. If it is exchangeable and
are the
same. If it is exchangeable and 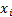 are
multivariate normal then we must have
are
multivariate normal then we must have 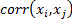 being the
same for all
being the
same for all 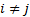 , say
, say 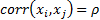 . This arises
if we set
. This arises
if we set 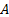 and
and 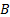 as
follows, if
as
follows, if 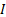 is the
identity matrix:
is the
identity matrix: