Finding The Most Important Principal
Component
[this page | pdf | back links]
Suppose we have a set of 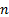 series
of returns (or losses, …). A principal component is a set of exposures (and a
principal component series is a series of returns) corresponding to an
eigenvector of the relevant
series
of returns (or losses, …). A principal component is a set of exposures (and a
principal component series is a series of returns) corresponding to an
eigenvector of the relevant 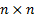 covariance
matrix,
covariance
matrix, 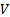 .
Eigenvectors satisfy the vector equation
.
Eigenvectors satisfy the vector equation 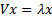 for
some scalar
for
some scalar 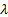 .
.
Typically principal components are identified in practice
using suitable software packages designed to identify eigenvectors and
eigenvalues, applied to the relevant covariance matrix, 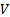 ,
e.g. using using Nematrian web services functions that target principal
components, i.e. MnPrincipalComponents,
MnPrincipalComponentsSizes
and MnPrincipalComponentsWeights.
,
e.g. using using Nematrian web services functions that target principal
components, i.e. MnPrincipalComponents,
MnPrincipalComponentsSizes
and MnPrincipalComponentsWeights.
However, for the first, i.e. most important, principal
component there is a conceptually simpler approach as follows.
We note that any vector can be written as a combination of
the eigenvectors of a matrix, and that these eigenvectors can be chosen to be
orthonormal (if suitably chosen if some eigenvalues take the same value) so we
can write any vector, 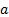 ,
of active positions as the sum of positions,
,
of active positions as the sum of positions, 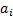 ,
in the relevant eigenvectors,
,
in the relevant eigenvectors, 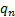 ,
i.e. as:
,
i.e. as:
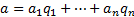
Then, 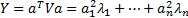 .
If we order the eigenvectors (principal components) so that the most important
ones are first, i.e.
.
If we order the eigenvectors (principal components) so that the most important
ones are first, i.e. 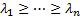 then
then
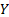 is
maximised, subject to
is
maximised, subject to 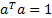 ,
if
,
if 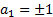 and
and
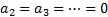 .
Thus, we can identify the most important principal component by reference to
the set of positions of unit magnitude that exhibit the largest risk (here
equated with ex-ante tracking error/variance/VaR).
.
Thus, we can identify the most important principal component by reference to
the set of positions of unit magnitude that exhibit the largest risk (here
equated with ex-ante tracking error/variance/VaR).