Enterprise Risk Management Formula Book
10. Portfolio optimisation
[this page | pdf | back links]
10.1 Mean-variance
portfolio optimisation
If there are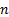 
asset
categories then a (one period) mean-variance efficient portfolio, 
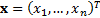where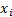 
is the
amount (or weight) invested in the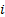 
’th asset,
given a benchmark,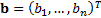 
, assumed
future (one period) mean returns on each asset,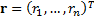 
, and an
assumed covariance matrix between the (one period) returns on different assets,
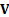, is a
portfolio that maximises the utility function,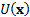 
for some
risk aversion parameter,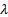 
, subject
to relevant constraints on the 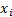, where:
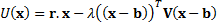
The constraints that are applied are usually linear, i.e. of
the form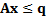 
which if 
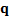is an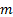 
dimensional
vector is understood as meaning that there are 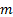constraints
each of the form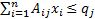 
. In such a
formulation, equality constraints, including that the amounts invested add up
to the total portfolio value (or the weights add to unity), can be written as
two inequality constraints, e.g.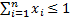 
and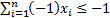 
combined.
The implied alphas with a mean-variance risk-return model
given a portfolio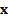 
and
benchmark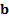 
are the
mean returns that need to be assumed for the different asset categories for 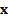to be
mean-variance optimal for some value of 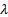. They can
only meaningfully be determined for assets whose weights in the portfolio are
not constrained (other than by the constraint that weights add to unity). They
are then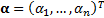 
where 
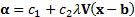where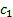 
and 
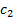are
arbitrary scalar constants.
10.2 Capital Asset Pricing Model (CAPM)
The security market line is:
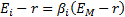
where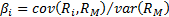 
The capital market line (for efficient portfolios) is:
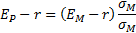
NAVIGATION LINKS
Contents | Prev | Next