Copulas – A short introduction
[this page | pdf | references | back links]
Copulas have become a more common risk management tool in
recent years because they provide a more complete means of characterising
co-dependency between series than merely correlation coefficients.
If different return series are coming from a multivariate
Normal distribution then their co-dependency characteristics are entirely
driven by their correlation matrix. A correlation coefficient of 1 corresponds
to perfectly positively correlated, 0 to be being uncorrelated and -1 to
completely negatively correlated). Whilst correlation is an important tool in
finance, correlation is not the same thing as ‘dependence’. Two series can on
average be ‘uncorrelated’ (across the distribution as a whole), but may still
be ‘correlated’ in the tail of the distribution (i.e. tend there to move in
tandem).
For risk management purposes we are often particularly
interested in extreme adverse events. In a portfolio context these will often
involve several very adverse factors coming together at the same time, i.e. we
are particularly interested in the extent to which factors driving portfolio
behaviour seem to be ‘correlated in the (downside) tail’ of the distribution.
The definition of a copula is a function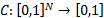 
where:
(a) There are
(uniform) random variables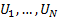 
taking
values in 
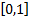such
that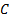 
is
their cumulative (multivariate) distribution function; and
(b) 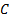has uniform
marginal distributions, i.e. for all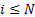 
and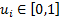 
we
have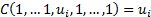 
The basic rationale for copulas is that any joint
distribution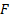 
of a set of random variables 
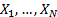i.e.
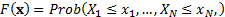can
be separated into two parts. The first is the combination of the marginal
distribution functions for each random variable in isolation, also called the marginals, i.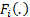e. 
where
.
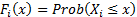The second is the copula that describes the dependence structure between
the random variables. Mathematically, this decomposition relies on Sklar’s
theorem, which states that if 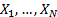are
random variables with marginal distribution functions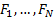 
and
joint distribution function 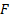then there exists an N-dimensional
copula 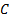such that for all 
:
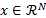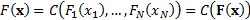
Copulas can be of any dimension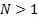 
. For example,
the co-depency between 3 different series cannot be encapsulated merely by 3
different elements characterising the co-dependency between each pair of
series. A quantum mechanical analogue would be the possibility that 3 different
quantum mechanical objects can be ‘entangled’ in more complex ways than is
possible merely by considering each pair in turn.
The simplest copulas are two-dimensional ones that
describe aspects of the co-depencency merely between two different
random variables. These are prototypical of more complicated copulas. Such a
copula, 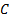, has the following properties:
(a) Its domain,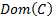 
,
i.e. the range of values for which it is defined, is a unit square, i.e.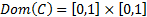 
(b) It adheres to
the following relationships:
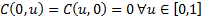
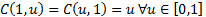
(c) It is ‘2-increasing’,
i.e.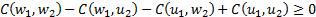 
whenever
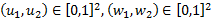and
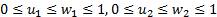
The copula function of random variables is invariant under a
strictly increasing transformation. Thus the copula completely encapsulates the
dependence characteristics between different random variables.
Certain relationships and limits can be derived on the
values that copulas can take. Fréchet copulas corresponding to the lower and
upper bounds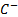 
and
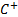are:
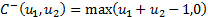
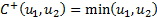
Any two-dimensional copula, 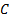, satisfies the
following ordering, which is called the concordance order (for distributions)
or the stochastic order (for random variables)
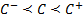
Another important special case is the product (or independence)
copula, see which is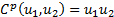 
.
Two random variables,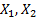 
are
said to be:
(a) countermonotonic
if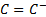 
(b) independent
if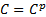 
(c) comonotonic
if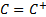 
Information on several of the above copulas (and on other
probability distributions) is available here,
including details of the following copulas: Clayton, Comonotonicity, Countermonotonicity,
Frank, Generalised
Clayton, Gumbel, Gaussian, Independence and t copulas.