Constrained Quadratic Optimisation: 3.
Setting up the ‘super’-problem
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next
page
3. Setting up the
‘super’-problem
To set up the superset of the original problem as described
in Solving
the canonical problem, we multiply through each row in the above tableau
(both left and right hand sides) by 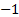 if the
relevant element of
if the
relevant element of 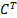 or
or 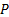 is
negative. This means that the right-hand side of the tableau is all now
non-negative. Simultaneously we introduce a further series of ‘artificial’
variables
is
negative. This means that the right-hand side of the tableau is all now
non-negative. Simultaneously we introduce a further series of ‘artificial’
variables 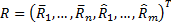 , all
elements of which are
, all
elements of which are 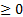 , the first
, the first 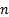 elements
of which,
elements
of which, 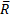 , are
artificial variables corresponding to the
, are
artificial variables corresponding to the 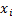 and the
remaining
and the
remaining 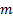 elements are
artificial variables corresponding to the
elements are
artificial variables corresponding to the 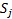 . To be more
precise, if we want the speediest algorithm, we only introduce only such elements
of these variables that are needed to achieve a starting feasible solution.
. To be more
precise, if we want the speediest algorithm, we only introduce only such elements
of these variables that are needed to achieve a starting feasible solution.
The starting solution is then given by 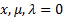 and:
and:
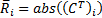
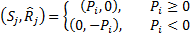
The starting ‘basic’ variables, i.e. those whose opening
values are greater than zero are each of the 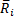 and
whichever of the
and
whichever of the 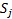 and the
and the 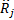 is non-zero
in the above formulae.
is non-zero
in the above formulae.
The complete starting tableau is then:
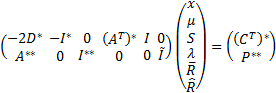
Subject to 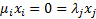 for
for  ,
,
 and
and 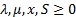 where
where
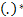 means
multiply through relevant row of the matrix by
means
multiply through relevant row of the matrix by 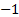 if
if
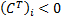 ,
, 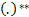 means
multiply through relevant row of the matrix by
means
multiply through relevant row of the matrix by 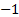 if
if
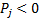 and
and 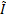 is the
is the 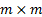 identity
matrix with each 1 replaced by a zero if the corresponding value of
identity
matrix with each 1 replaced by a zero if the corresponding value of 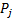 is greater
than zero.
is greater
than zero.
N.B. We have ignored for the purposes of this discussion the
possibility that any of the entries on the right-hand side of the tableau are
identically zero. This degenerate case can be handled by adding a very small
number to make them positive.
We need to know which variables ‘correspond’ to each other
(i.e. appear jointly in the constraints 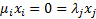 , although
these correspondences do not change as the iteration progresses.
, although
these correspondences do not change as the iteration progresses.
In addition to the Tableau, which is an 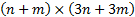 array we
also need to keep track of the following as the iteration proceeds:
array we
also need to keep track of the following as the iteration proceeds:
Two rows:
(a) BasicRow,
indicates with, say, a 1 whether the variable in question is ‘basic’
(b) ObjectiveRow,
initially calculated as:
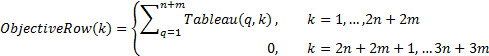
Two columns:
(c) SolutionColumn,
contains the current feasible solution, i.e. the right hand side of the above
tableau ‘equation’; and
(d) BasicColumn,
contains integers indicating to which variables the entries in the SolutionColumn
currently apply (and thus which variables are basic, so there is some overlap
here with BasicRow). BasicColumn starts as:
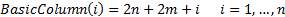
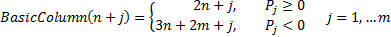
NAVIGATION LINKS
Contents | Prev | Next