Constrained Quadratic Optimisation: 1.
The canonical problem
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next
page
1. The canonical
problem
Constrained quadratic optimisation involves finding the
value of a vector 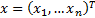 that
minimises a given penalty function
that
minimises a given penalty function 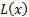 (or
maximises it, the two are interchangeable by replacing
(or
maximises it, the two are interchangeable by replacing 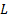 with
with
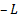 ) subject to
some (normally linear) constraints, where:
) subject to
some (normally linear) constraints, where:
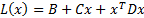
The constraints, in canonical form, are normally of two
types. There are 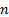 lower limit
constraints of the form
lower limit
constraints of the form 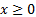 (by which we
mean that each
(by which we
mean that each 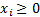 for
for 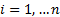 )
and there are
)
and there are 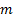 further
constraints of the form
further
constraints of the form 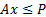 (by which we
mean that each
(by which we
mean that each 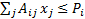 for
for 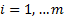 ).
).
In these definitions 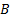 is a scalar,
is a scalar,
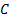 is a vector
(or
is a vector
(or 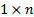 matrix) and
matrix) and 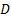 is
an
is
an 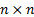 symmetric
matrix, which is assumed to be non-positive definite if the problem is a
minimisation, and non-negative definite if the problem is a maximisation. A
non-negative definite (symmetric) matrix is one whose eigenvalues are all at
least zero.
symmetric
matrix, which is assumed to be non-positive definite if the problem is a
minimisation, and non-negative definite if the problem is a maximisation. A
non-negative definite (symmetric) matrix is one whose eigenvalues are all at
least zero.
The value of 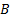 is
irrelevant to the optimal value of
is
irrelevant to the optimal value of 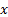 so without
loss of generality can be taken as zero.
so without
loss of generality can be taken as zero.
Problems with lower limits on each 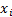 that are
non-zero, say
that are
non-zero, say 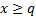 can be
restated into the above form by a change of variables to
can be
restated into the above form by a change of variables to 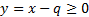 resulting
in a new penalty function:
resulting
in a new penalty function:
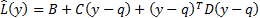
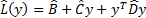
Here 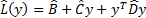 where
where 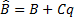 ,
, 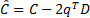 and
and 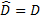 . We
therefore merely need to alter
. We
therefore merely need to alter 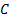 appropriately,
and unwind the change of variables at the end of the optimisation process.
appropriately,
and unwind the change of variables at the end of the optimisation process.
Problems that involve ‘greater than’ or ‘equals’ type
constraints, e.g. 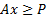 or
or 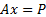 as
well as (or instead of) ‘less than’ type constraints can be converted into the
above canonical form by:
as
well as (or instead of) ‘less than’ type constraints can be converted into the
above canonical form by:
(a) converting each
‘equality’ constraint into two equivalent constraints, one being the
corresponding ‘greater than’ constraint and one being the corresponding ‘less
than’ constraint, altering 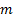 accordingly
(since if
accordingly
(since if 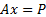 then
then 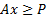 and
and
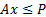 , and then
, and then
(b) inverting each
‘greater than’ constraint present into a ‘less than’ constraint by noting that
if 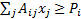 then
then 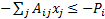 .
.
NAVIGATION LINKS
Contents | Prev | Next