The Chi-squared distribution
[this page | pdf | back links]
The chi-squared distribution with 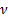 degrees
of freedom is the distribution of a sum of the squares of
degrees
of freedom is the distribution of a sum of the squares of 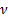 independent
standard normal random variables. A consequence is that the sum of independent
chi-squared variables is also chi-squared distributed. It is widely used in
hypothesis testing, goodness of fit analysis or in constructing confidence
intervals. It is a special case of the gamma distribution.
independent
standard normal random variables. A consequence is that the sum of independent
chi-squared variables is also chi-squared distributed. It is widely used in
hypothesis testing, goodness of fit analysis or in constructing confidence
intervals. It is a special case of the gamma distribution.
![[SmartChart]](I/ChiSquaredDistribution_files/image002.gif)
![[SmartChart]](I/ChiSquaredDistribution_files/image003.gif)
![[SmartChart]](I/ChiSquaredDistribution_files/image004.gif)
|
Distribution name
|
Chi-squared
distribution
|
|
Common notation
|
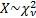
|
|
Parameters
|
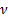 =
degrees of freedom (positive integer) =
degrees of freedom (positive integer)
|
|
Domain
|
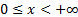
|
|
Probability density
function
|
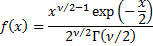
|
|
Cumulative distribution
function
|
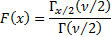
|
|
Mean
|
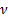
|
|
Variance
|
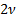
|
|
Skewness
|
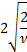
|
|
(Excess) kurtosis
|
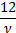
|
|
Characteristic function
|
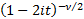
|
|
Other comments
|
Its median is approximately 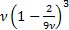 . Its mode is . Its mode is 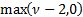 . Is also known as the
central chi-squared distribution (when there is a need to contrast it with
the noncentral chi-squared distribution). . Is also known as the
central chi-squared distribution (when there is a need to contrast it with
the noncentral chi-squared distribution).
In the special case of 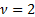 the cumulative
distribution function simplifies to the cumulative
distribution function simplifies to 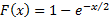 . .
As 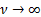 , , 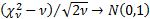 and and 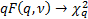
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “chi-squared”.
Functions relating to a generalised version of this distribution including
additional location (i.e. shift) and scale parameters may be accessed by using
a DistributionName of “chi-squared3” ”, see also including
additional shift and scale parameters. For details of other supported
probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next