The Cauchy distribution
[this page | pdf | back links]
![[SmartChart]](I/CauchyDistribution_files/image001.gif)
![[SmartChart]](I/CauchyDistribution_files/image002.gif)
![[SmartChart]](I/CauchyDistribution_files/image003.gif)
|
Distribution name
|
Cauchy
distribution
|
|
Common notation
|
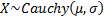
|
|
Parameters
|
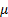 =
location parameter =
location parameter
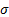 = scale
parameter ( = scale
parameter (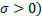
|
|
Domain
|
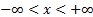
|
|
Probability density
function
|
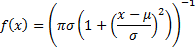
|
|
Cumulative distribution
function
|

|
|
Mean
|
Does not exist
|
|
Variance
|
Does not exist
|
|
Skewness
|
Does not exist
|
|
(Excess) kurtosis
|
Does not exist
|
|
Characteristic function
|
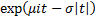
|
|
Other comments
|
The quantile function of the Cauchy distribution is:
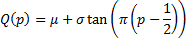
Its median is thus 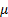 . .
The Cauchy distribution is a special case of the stable (more
precisely the sum stable) distribution family.
The special case of the Cauchy distribution when 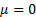 and and 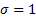 is
called the standard Cauchy distribution. It coincides with the Student’s t
distribution with one degree of freedom. It has a probability density
function of is
called the standard Cauchy distribution. It coincides with the Student’s t
distribution with one degree of freedom. It has a probability density
function of 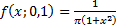 . .
If 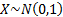 and and
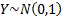 are
independent random variables then are
independent random variables then 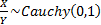 and this can be used to
generate random variates. and this can be used to
generate random variates.
The Cauchy distribution is also known as the
Cauchy-Lorentz or Lorentz distribution (especially amongst physicists).
|
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “cauchy”. For
details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next