/

Formulae for prices and Greeks for European (vanilla) calls in a Black-Scholes world

[this page | pdf | references | back links]

See Black Scholes Greeks for notation.

 

Payoff, see MnBSCallPayoff

 

 

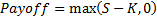
Price (value), see MnBSCallPrice

 

 

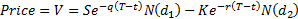
Delta (sensitivity to underlying), see MnBSCallDelta

 

 

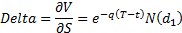
Gamma (sensitivity of delta to underlying), see MnBSCallGamma

 

 

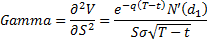
Speed (sensitivity of gamma to underlying), see MnBSCallSpeed

 

 

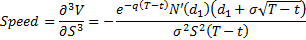
Theta (sensitivity to time), see MnBSCallTheta

 

 

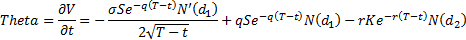
Charm (sensitivity of delta to time), see MnBSCallCharm

 

 

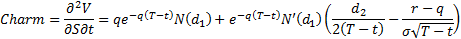
Colour (sensitivity of gamma to time), see MnBSCallColour

 

 

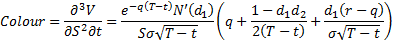
Rho(interest) (sensitivity to interest rate), see MnBSCallRhoInterest

 

 

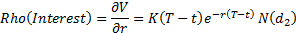
Rho(dividend) (sensitivity to dividend yield), see MnBSCallRhoDividend

 

 

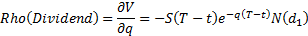
Vega (sensitivity to volatility), see MnBSCallVega}*

 

 

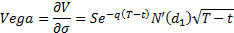
Vanna (sensitivity of delta to volatility), see MnBSCallVanna*

 

 

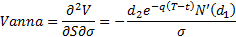
Volga (or Vomma) (sensitivity of vega to volatility), see MnBSCallVolga*

 

 

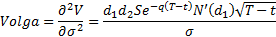
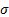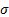* Greeks like vega, vanna and Volga/vomma that involve partial differentials with respect to  are in some sense ‘invalid’ in the context of Black-Scholes, since in its derivation we assume that  is constant. We might interpret them as applying to a model in which 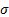 was slightly variable but otherwise was close to constant for all 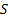,  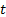etc.. Vega, for example, would then measure the sensitivity to changes in the mean level of . 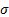For some types of derivatives, e.g. binary puts and calls, it can be difficult to interpret how these particular sensitivities should be understood.

 

---