The binomial distribution
[this page | pdf | back links]
The binomial distribution 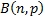 is
the discrete probability distribution applicable to the number of successes in
a sequence of
is
the discrete probability distribution applicable to the number of successes in
a sequence of 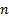 independent yes/no
experiments each of which has a success probability of
independent yes/no
experiments each of which has a success probability of 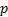 . Each
individual success/failure experiment is called a Bernoulli trial, so if
. Each
individual success/failure experiment is called a Bernoulli trial, so if 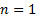 then the
binomial distribution is a Bernoulli
distribution.
then the
binomial distribution is a Bernoulli
distribution.
It has the following characteristics:
|
Distribution name
|
Binomial
distribution
|
|
Common notation
|
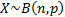
|
|
Parameters
|
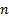 =
number of (independent) trials, positive integer =
number of (independent) trials, positive integer
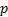 =
probability of success in each trial, =
probability of success in each trial, 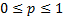
|
|
Support
|

|
|
Probability mass
function
|
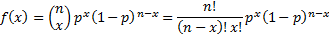
|
|
Cumulative distribution
function
|
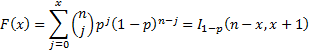
|
|
Mean
|
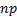
|
|
Variance
|
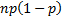
|
|
Skewness
|
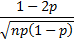
|
|
(Excess) kurtosis
|
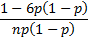
|
|
Characteristic function
|
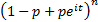
|
|
Other comments
|
The Bernoulli
distribution is 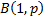 and corresponds to the
likelihood of success of a single experiment. Its probability mass function
and cumulative distribution function are: and corresponds to the
likelihood of success of a single experiment. Its probability mass function
and cumulative distribution function are:
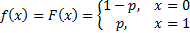
The Bernoulli distribution with 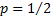 , i.e. , i.e. 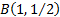 , has the minimum
possible excess kurtosis, i.e. , has the minimum
possible excess kurtosis, i.e. 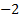 . .
The mode of 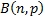 is is 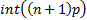 if if 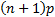 is 0 or not an integer
and is is 0 or not an integer
and is 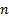 if if 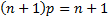 . If . If 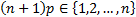 then the distribution
is bi-modal, with modes then the distribution
is bi-modal, with modes 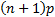 and and 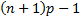 . .
|
The binomial distribution is often used to model the number
of successes in a sample size of 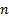 from a population size of
from a population size of
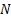 .
Since such samples are not independent, the resulting distribution is actually
a hypergeometric distribution and not a binomial distribution. However if
.
Since such samples are not independent, the resulting distribution is actually
a hypergeometric distribution and not a binomial distribution. However if 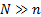 then
the binomial distribution becomes a good approximation to the relevant
hypergeometric distribution and is thus often used.
then
the binomial distribution becomes a good approximation to the relevant
hypergeometric distribution and is thus often used.
In the above 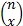 is
the binomial
coefficient.
is
the binomial
coefficient.
Nematrian web functions
Functions relating to the above distribution may be accessed
via the Nematrian
web function library by using a DistributionName of “binomial”. For
details of other supported probability distributions see here.
NAVIGATION LINKS
Contents | Prev | Next