Demonstrating that VaR (for worse enough
outcomes) is a coherent risk measure for a Gaussian, i.e. multi-variate normal,
distribution
[this page | pdf | references | back links]
For a risk measure to be coherent it must satisfy:
(a) Subadditivity:
for any pair of loss variables, 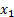 and
and 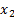
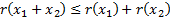
(b) Monotonicity:
if, for all states of the world, 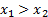 then
then
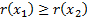
(c) Homogeneity:
for any constant 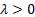 and random loss
variable
and random loss
variable 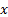
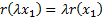
(d) Translational invariance:
for any constant 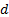 and random loss
variable x
and random loss
variable x
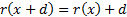
For a normal distribution the VaR at the 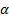 confidence
level is as follows, if the distribution (for the given variable of interest)
is distributed
confidence
level is as follows, if the distribution (for the given variable of interest)
is distributed 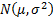 :
:
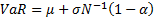
Homogeneity and translational invariance therefore
immediately apply.
Subadditivity holds (as long as 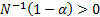 , i.e.
, i.e. 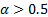 )
because the standard deviation of the sum of two random variables is less than
or equal to the sum of their standard deviations
)
because the standard deviation of the sum of two random variables is less than
or equal to the sum of their standard deviations
Monotonicity holds because Normally distributed random
variables have positive support on the
real line, so 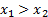 in all states
of the world only if
in all states
of the world only if 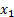 and
and 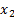 are perfectly
correlated, in which case
are perfectly
correlated, in which case 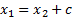 , where
, where 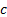 is
constant, hence
is
constant, hence 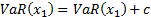 for any
for any 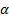 .
.