Value-at-Risk
[this page | pdf | references | back links]
The Value-at-Risk, VaR, of a portfolio 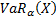 is
the outcome (loss),
is
the outcome (loss), 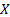 , that will be exceeded on a
fraction
, that will be exceeded on a
fraction 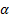 of occasions. It requires a
time-scale (
of occasions. It requires a
time-scale (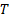 ) as well as a confidence level
) as well as a confidence level 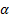 .
.
Where the support of the
distribution is continuous, the Value-at-Risk with confidence level 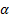 is:
is:
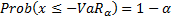
If the distribution is unbounded below then this means that
if the probability density function of the distribution is 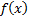 we
have:
we
have:
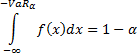
If the lower bound is finite, e.g. 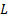 then the
definition would replace
then the
definition would replace 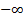 with
with 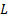 .
.
Note: sometimes 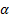 and
and 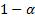 are
interchanged or losses are deemed positive rather than negative etc.
are
interchanged or losses are deemed positive rather than negative etc.
Visually the difference between VaR and Tail VaR (TVaR) may be
seen in either of the following charts:
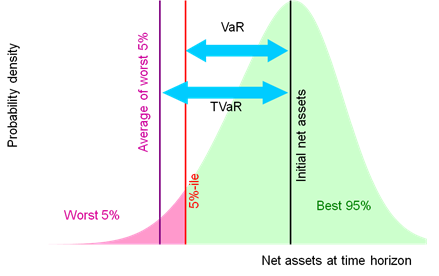
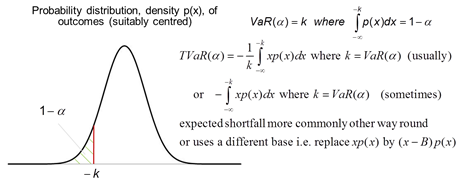
VaR is not (in general) a coherent risk
measure, whilst TVaR is. VaR is arguably more shareholder focused and TVaR more
regulator/customer focused, see VaR versus TVaR mindsets.
If several different risk exposures are contributing to the
overall VaR then it often becomes important to identify the contribution each
is making to the total. This can be done using marginal Value-at-Risk.