Standard Statistical Tests for normality
[this page | pdf | back links]
Standard statistical tests for identifying whether an
observed sample is likely not to have come from a normal distribution include:
(a) Testing the
extent to which the skew of the sample is non-zero, see e.g. Confidence
level for skew for large sample normal distribution
(b) Testing the extent to
which the (excess) kurtosis of the sample is non-zero, see e.g. Confidence
level for (excess) kurtosis for large sample normal distribution
(c) The Jarque-Bera
test which simultaneously tests the extent to which the skew and (excess)
kurtosis of the sample are non-zero
(d) The Shapiro-Wilk test
(e) The Anderson-Darling test*
(f) The Kolmogorov-Smirnov
test*
(g) The Cramer-von-Mises test*
* These tests can be used with any distributional form, i.e.
they are not limited to testing merely for non-normality. Their test statistics
depend on the sample data through terms that depend merely on order statistics
and then only on how these map onto the hypothesised cumulative distribution
function (i.e. if the sample is 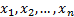 then
merely through
then
merely through 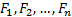 where
where
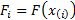 where
where
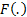 is
the cumulative distribution function and
is
the cumulative distribution function and 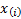 is
the
is
the 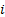 ’th order statistic, i.e. the
’th order statistic, i.e. the
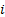 ’th
smallest value in the sample). In contrast (a) to (c) are parametric, with
their test statistics depending merely on specific moments of the distribution
(here the skew and kurtosis and the two combined respectively). (d) depends on
both order and parametric elements.
’th
smallest value in the sample). In contrast (a) to (c) are parametric, with
their test statistics depending merely on specific moments of the distribution
(here the skew and kurtosis and the two combined respectively). (d) depends on
both order and parametric elements.
All of the above tests, as conventionally formulated, have
the disadvantage that they give ‘equal’ weight to every observation. A possible
exception is the Kolmogorov-Smirnov test, which merely refers to the single
(ordered) observation that appears to exhibit the greatest deviation from where
we might have expected it lie.
As explained in Kemp (2009),
this generally means that they indicate mainly whether a sample appears to be
deviating from normality in the middle of the distribution rather than whether
it appears to be deviating from normality in its tails. Loosely speaking, this
is because there are far more observations in the middle of a normal
distribution than in its tail. We illustrate this with (b). Consider the
proportion of observations that are in the tails of a normal distribution. Only
approximately 1 in 1.7 million observations from a normal distribution should
be further away from the (sample) mean than 5 standard deviations. Each one in
isolation might on average contribute at least 625 times as much to the
computation of kurtosis as an observation that is just one standard deviation
away from the (sample) mean (since 5 x 5 x 5 x 5 = 625), but, because there are
so few observations this far into the tail, they in aggregate have little
impact on the overall kurtosis of the distribution.
Better, if we are interested merely in testing for deviation
from normality in a part of a distributional form is to modify the above
methodologies so that they depend just on data from the relevant part of the
observed distributional form. For example, we might wish to focus on the worst
10% of outcomes. We would then estimate the mean and standard deviation of a normal
distribution that would have its worst 10% of outcomes as close as possible to
those actually observed, and we would then apply a modified test statistic that
referred merely to the observations in the part of the distributional form in
which we are interested. In general, we can view this modification as involving
giving different weights 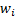 to
the different
to
the different 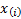 .
To calculate critical values for such statistics (and therefore whether or not
to reject the null hypothesis of normality) generally requires Monte Carlo
simulation techniques, given the wide range of possible weighting schemas that
could be used.
.
To calculate critical values for such statistics (and therefore whether or not
to reject the null hypothesis of normality) generally requires Monte Carlo
simulation techniques, given the wide range of possible weighting schemas that
could be used.
NAVIGATION LINKS
Contents | Next