Special polynomials
[this page | pdf]
A (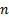 ’th order) polynomial is a
function of the form
’th order) polynomial is a
function of the form 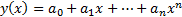 where
the
where
the 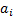 are
constant. They appear in many guises in mathematics. Whilst it is common to
focus on cases where
are
constant. They appear in many guises in mathematics. Whilst it is common to
focus on cases where 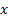 is a real number, there are
attractions in extending their domain to relate to complex numbers,
with the
is a real number, there are
attractions in extending their domain to relate to complex numbers,
with the 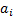 also
then being allowed to be complex. For example, a polynomial of order
also
then being allowed to be complex. For example, a polynomial of order 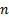 always
then has
always
then has 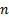 (possibly not distinct)
roots, i.e. values of
(possibly not distinct)
roots, i.e. values of 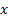 where
where 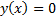 but
even if all the
but
even if all the 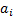 are
real some of these roots may be complex.
are
real some of these roots may be complex.
Several special types of polynomial have been widely
analysed, including:
-
Legendre polynomials
-
Chebshev polynomials
-
Hermite polynomials
-
Jacobi polynomials
-
Laguerre polynomials
These polynomials all appear in a natural way when we try to
approximate a functional form as follows.
Suppose we define a space of real or complex valued
(continuous) functions on the interval 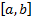 .
A natural ‘scalar product’ of two functions
.
A natural ‘scalar product’ of two functions 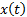 and
and
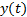 is
then:
is
then:
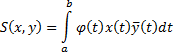
where 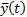 is
the complex conjugate
of
is
the complex conjugate
of 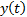 and
and
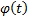 is
a real continuous non-negative function (with at most finitely many zeros)
called the weight function for the given scalar product. If the
is
a real continuous non-negative function (with at most finitely many zeros)
called the weight function for the given scalar product. If the 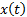 and
and
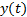 are
limited to real functions then the definition simplifies to the folloing
(because the same formulae apply, but the complex
are
limited to real functions then the definition simplifies to the folloing
(because the same formulae apply, but the complex
We may then, for example, define 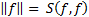 .
If
.
If 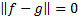 then
then
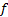 and
and
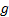 are
then identical (if continuous) within the interval
are
then identical (if continuous) within the interval 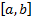 .
We also have
.
We also have 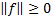 for
all
for
all 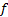 , so we can view
, so we can view 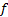 as a good
approximation to
as a good
approximation to 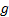 if
if 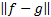 is
close to zero. Different weight functions then indicate where within the
interval
is
close to zero. Different weight functions then indicate where within the
interval 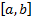 we
most want the approximation to be accurate.
we
most want the approximation to be accurate.
As with any vector space, we can define a basis of
orthogonal elements, 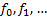 (which
is here infinite dimensional) which in aggregate ‘span’ the entire vector
space, i.e. here the entire range of (continuous) functions defined on
(which
is here infinite dimensional) which in aggregate ‘span’ the entire vector
space, i.e. here the entire range of (continuous) functions defined on 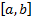 .
By orthogonal we mean
.
By orthogonal we mean 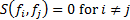 .
The different special functions listed above provide natural orthogonal bases
for different weight functions:
.
The different special functions listed above provide natural orthogonal bases
for different weight functions:
Legendre: 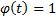 and
and
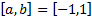 (can
also be viewed as a special case of Jacobi with
(can
also be viewed as a special case of Jacobi with 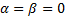 )
)
Jacobi: 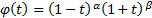 and
and
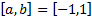
Chebyshev: the special case of the Jacobi with 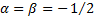 which
means that they can be expressed in a simple analytical manner.
which
means that they can be expressed in a simple analytical manner.
Laguerre: 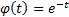 and
and
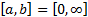
Hermite: 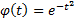 and
and
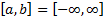
For example, the first few Legendre polynomials are 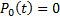 ,
,
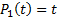 ,
,
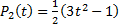 ,
,
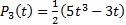 ,
…
,
…
The exact definition of each special polynomial type depends
on the ‘normalisation’ used. This is because if 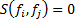 then
then
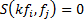 for
any
for
any 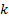 . The usual normalisation
convention involves
. The usual normalisation
convention involves 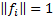 for
all
for
all 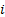 .
.
In the financial world, the computation of many types of
risk measures is mathematically akin to a evaluating a particular integral. A
common way of carrying out numerical integration is to use an approach called
Gaussian quadrature. This is often implemented in a fashion that makes use of
some of the polynomials described above.