Quantitative Return Forecasting
5. Chaotic market behaviour
[this page | pdf | references | back links]
Return to Abstract and
Contents
Next page
5.1 To achieve chaotic behaviour (at least
chaotic as defined mathematically) we need to drop the assumption of time
stationarity, in some shape or form. This does not mean that we need to drop
time predictability. Instead it means that the equation governing the behaviour
of the system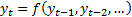 
involves
a non-linear function 
.
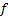5.2 This change can create quite radically
different behaviour. Take for example the logistic map or quadratic
map: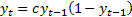 
where
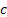is
constant. This mapping can also be thought of as a special case of generalised
least squares regression (but not generalised linear least squares
regression), in the sense that we can find 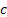by
carrying out a suitable regression analysis where one of the function is a
quadratic. In this equation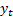 
depends
deterministically on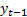 
and
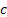is
a parameter that controls the qualitative behaviour of the system, ranging from
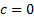which
generates a fixed point (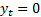
)
to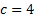 
where each iteration in
effect destroys one bit of information.
5.3 To understand the behaviour when 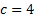, we note
that if we know the value to within e (e small) at one iteration then we will only
know the position within 2e at the next
iteration. This exponential increase in uncertainty or divergence of nearby
trajectories is what is generally understood by the term deterministic chaos.
This behaviour is quite different to that produced by traditional linear
models. Any broadband component in the power spectrum output of a traditional
linear model has to come from external noise. With non-linear systems such
output can be purely deterministically driven (and therefore in some cases
predictable). The above example also shows that the systems do not need to be
complicated to generate chaotic behaviour.
5.4 The main advantages of such non-linear models
are that many factors influencing market behaviour can be expected to do so in
a non-linear fashion and the resultant behaviour matches observations, e.g.
markets often seem to exhibit cyclical behaviour, but with the cycles having no
set lengths, and markets are often relatively little affected by certain
drivers in some circumstances, but affected much more by the same drivers in
other circumstances.
5.5 The main disadvantages of non-linear models
are:
(a)
The mathematics is more complex;
(b)
Modelling underlying market dynamics in this way will make the modelling
process less efficient if the underlying dynamics are in fact linear in nature;
and
(c)
If markets are chaotic, then this typically places fundamental limits on
the ability of any approach to predict more than a few time steps ahead.
5.6 The last point arises because chaotic
behaviour is characterised by small disturbances being magnified over time in
an exponential fashion (as per the quadratic map described above with ),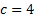
eventually swamping the predictive power of any model that can be built up. Of
course, in these circumstances using linear approaches may be even less
effective!
5.7 Indeed, there are purely deterministic
non-linear models that are completely impossible to use for predictive purposes
even one step ahead. Take for example a situation in which there is a hidden
state variable developing according to the following formula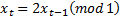 
but we can only observe ,
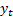the integer nearest to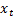 
.
The action of the map is most easily understood by writing 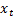in
a binary fractional expansion, i.e.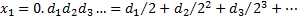 
.
Each iteration shifts every digit to the right, so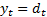 
.
Thus this system successively reveals each digit in turn. Without prior
knowledge of the seeding value, the output will appear to be completely random,
and the past values of 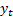available
at time 
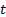tell us nothing at all
about values at later times!
NAVIGATION LINKS
Contents | Prev | Next