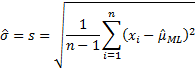Maximum Likelihood Estimation of Normal
Distribution
[this page | pdf]
The probability density (likelihood) of a single variable
drawn from a Normal distribution 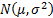 is:
is:
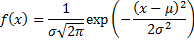
Thus the likelihood of 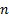 independent
draws
independent
draws 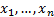 from
this distribution is:
from
this distribution is:
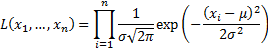
To identify the values of 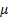 and
and 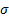 that maximise
that maximise 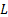 it is easiest to
identify the maximum of the log likelihood (as the two will be maximised for
the same values of
it is easiest to
identify the maximum of the log likelihood (as the two will be maximised for
the same values of 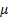 and
and 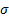 since
since 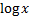 is
a monotonically increasing function of
is
a monotonically increasing function of 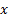 ).
The log likelihood is:
).
The log likelihood is:
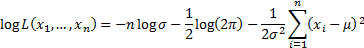
This is maximised when 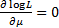 and
and
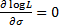 ,
i.e. when:
,
i.e. when:
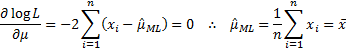
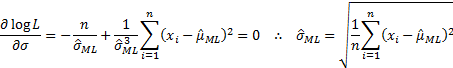
The maximum likelihood estimator, 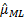 ,
of the mean
,
of the mean 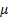 is thus the average of the
observations,
is thus the average of the
observations, 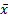 .
It is possible to show that this is also the minimum variance unbiased
estimator of
.
It is possible to show that this is also the minimum variance unbiased
estimator of 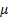 . The maximum likelihood estimator,
. The maximum likelihood estimator,
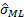 ,
of
,
of 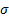 is
the population standard deviation,
is
the population standard deviation, 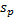 of
the
of
the 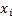 which
can be determined using the MnPopulationStdev
web function. Please note that whilst
which
can be determined using the MnPopulationStdev
web function. Please note that whilst 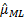 is
an unbiased estimator of
is
an unbiased estimator of 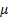 ,
, 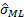 is
a biased estimator of
is
a biased estimator of 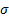 . The minimum variance unbiased
estimator of
. The minimum variance unbiased
estimator of 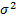 is
the sample variance (i.e. square of the sample standard
deviation). The sample standard deviation is:
is
the sample variance (i.e. square of the sample standard
deviation). The sample standard deviation is: