WeightedPercentile
[this page | pdf | back links]
Function Description
Returns 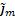 ,
the m’th weighted percentile (
,
the m’th weighted percentile (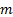 here being between 0 and
1) of a series of observations series
here being between 0 and
1) of a series of observations series 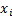 given
weights
given
weights 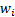 (for
(for
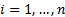 ).
).
Different commentators use different ways of identifying
percentiles (i.e. quantiles) from finite sized samples. See MnPercentile and MnPercentileExc for
details of how the Nematrian website calculates equally-weighted percentiles,
which match the approaches used by Microsoft.
For weighted percentiles, the Nematrian website uses
the following approach, which is not fully compatible with the approach it uses
for unweighted percentiles:
-
First sort the series in ascending order
-
Next build up a cumulative distribution based on the weights, and assume
that the percentile points for the mid-points of each bin are the 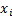 in
question (so, if the weight of the first in the ordered list is
in
question (so, if the weight of the first in the ordered list is 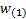 then
the
then
the 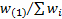 ’th
percentile is deemed to be exactly
’th
percentile is deemed to be exactly 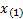 ,
the
,
the 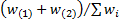 ’th percentile is deemed
to be exactly
’th percentile is deemed
to be exactly 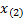 ,
etc.)
,
etc.)
-
Finally use linear interpolation as per the MnLinearInterpolation
function to interpolate remaining percentiles.
The MnLinearInterpolation
function does not extrapolate beyond the minimum and maximum values, so the
0’th and 1’th quantiles should be the minimum and maximum values of the series,
and hence be consistent with what would be returned for these quantile values
by the MnPercentile
function. However, intermediate values with the 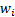 all
equal will not correspond exactly to those that would be returned by the MnPercentile function.
all
equal will not correspond exactly to those that would be returned by the MnPercentile function.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Statistical functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement