SudokuSolve
[this page | pdf | back links]
Function Description
Returns the solution to a Sudoku-style puzzle if given input
in a suitable form. See also Standard Sudoku Solver
and Killer Sudoku
Solver, which provide interactive ways of accessing this tool.
The easiest way to understand the required input format is
to consider the nature of a Killer Sudoku puzzle. In this Sudoku-variant, there
are various groupings of cells scattered across the 9 by 9 grid (usually
contiguous). These each have defined numbers of cells within them and a defined
total (e.g. there might be a grouping of 2 cells the total of which needs to be
3 (and thus the first cell of the pair forming this group can only be 1 and the
second 2 or vice-versa). Each entry in a group needs to be different, so there
are at most 9 cells in any one group. For, say, the 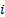 ’th group, we
thus know at outset the number of cells,
’th group, we
thus know at outset the number of cells, 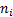 ,
in the group, the sum of the entries,
,
in the group, the sum of the entries, 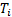 ,
of the cells in the group and the coordinates of each cell,
,
of the cells in the group and the coordinates of each cell, 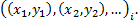
The required input form involves an array of bytes, in
groups of 20 consecutive entries (so if there are 30 groups then the input
array needs to be 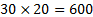 entries
long), ordered as follows:
entries
long), ordered as follows:
-
First entry = number of cells in the group, i.e. 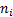
-
Second entry = required sum of entries in these cells, i.e. 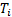
-
Third entry = 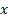 -coordinate of the first cell in
the group, i.e.
-coordinate of the first cell in
the group, i.e. 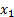
-
Fourth entry = 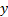 -coordinate of the first cell in
the group, i.e.
-coordinate of the first cell in
the group, i.e. 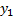
-
Fifth entry = 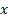 -coordinate of the second cell in
the group, i.e.
-coordinate of the second cell in
the group, i.e. 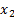
-
Sixth entry = 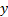 -coordinate of the second cell in
the group, i.e.
-coordinate of the second cell in
the group, i.e. 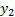 ,
etc. (with the last entries in the group of 20 ignored if the group has less
than 9 cells in it).
,
etc. (with the last entries in the group of 20 ignored if the group has less
than 9 cells in it).
Also takes as a further input the type of the Sudoku puzzle
(i.e. ‘Killer’, ‘Standard’, ‘Samurai’ or ‘General’). These simplify the inputs
(for the first three) so that you do not need each time to specify the standard
features of the puzzle. For example, with a Killer Sudoku puzzle, we can think
of the overarching grid layout as defining a further set of groups, since each
row, column and principal 3-by-3 group needs to contain all the numbers 1 to 9.
They can therefore be coded as akin to a group like the one above but with 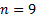 ,
, 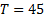 and the
remaining entries in the set of 20 consecutive bytes defining the positioning
of each cell (from 1 to 9). If you choose the ‘General’ type you will need to
enter these groups yourself. The solver will also not then check the input data
for consistency (e.g. with a Killer Sudoku puzzle all cell coordinates in the 9
by 9 grid need to be in the range 1 to 9, each cell needs to appears just once
in the definition of groups as above, and the sum of all of the group totals is
405).
and the
remaining entries in the set of 20 consecutive bytes defining the positioning
of each cell (from 1 to 9). If you choose the ‘General’ type you will need to
enter these groups yourself. The solver will also not then check the input data
for consistency (e.g. with a Killer Sudoku puzzle all cell coordinates in the 9
by 9 grid need to be in the range 1 to 9, each cell needs to appears just once
in the definition of groups as above, and the sum of all of the group totals is
405).
With a ‘Standard’ Sudoku puzzle, the same input format is
used as above. Each known entry in the grid forms corresponds to its own group,
with 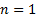 ,
, 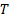 = the (known)
entry in the cell, and
= the (known)
entry in the cell, and 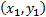 identifying
the location of that cell.
identifying
the location of that cell.
‘Samurai’ Sudoku involves a more complex grid, but can be
solved in a similar fashion, just with more initial groups.
The solver uses an exhaustive search approach, so should
identify a unique solution if there is one. However, it does include an
iteration upper limit which you might need to set reasonably high for more
complicated puzzles.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Mathematical puzzle functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement