StandardWeightedCubicQuantileFit
[this page | pdf | back links]
Function Description
Returns an array corresponding to a weighted cubic curve fit
to observed quantile values, where the weights correspond to the distance
between consecutive points (so that the fit gives greater weight to the tails
of the distribution). Requires as inputs an ordered array of 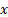 values
(e.g. expected quantiles, as per MnStandardisedNormalQuantiles
and an ordered array of
values
(e.g. expected quantiles, as per MnStandardisedNormalQuantiles
and an ordered array of 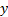 values
corresponding to the actually observed values.
values
corresponding to the actually observed values.
The curve fit is derived using the Nematrian least squares
generalised curve fit MnLeastSquaresGeneralisedCurveFit,
(specifically the polynomial
version).
The weights, 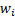 , used in
this function, if the ordered
, used in
this function, if the ordered 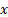 -values are
-values are 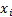 and there
are
and there
are 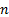 such
values, are:
such
values, are:
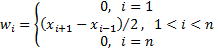
This potentially under allows for the two end points. An
alternative that gives greater weight to the two end points is MnStandardWeightedCubicQuantileFitInclEnds.
Please bear in mind that a cubic is not always a valid form
for a quantile-quantile function to take (e.g. if the slope of the cubic
becomes negative anywhere). If you wish to avoid this problem then we suggest
fitting a distributional form using e.g. (weighted) maximum likelihood, see
e.g. MnProbDistWeightedMLE.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Statistical functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement