Gamma
[this page | pdf | references | back links]
Function Description
The gamma function, 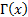 is
defined as:
is
defined as:
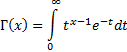
The gamma function can be thought of as the extension of the
factorial to the entire real (or complex) number set. For non-negative integers
it is merely the familiar factorial function, 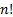 , but offset by 1,
i.e.
, but offset by 1,
i.e. 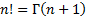 .
Like factorials, it satisfies the following recurrence relationship:
.
Like factorials, it satisfies the following recurrence relationship:
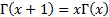
The Nematrian website approximates the gamma function using
a so-called Lanczos
approximation, see also Press et
al. (2007), Toth (2004) or
Wikipedia:
Lanczos approximation.
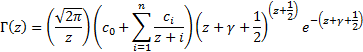
The particular Lanczos approximation the Nematrian website
uses involves:
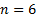
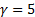
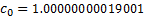
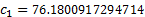
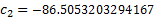
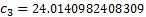
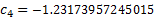
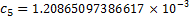
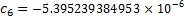
For large 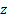 there is a risk of overflow, which can
be mitigated by using the MnLogGamma
function, defined as
there is a risk of overflow, which can
be mitigated by using the MnLogGamma
function, defined as 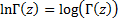 .
.
The Lanczos approximation is valid for arguments in the
right complex half-plane, but can be extended to the entire complex plane
(where the function is not singular) using the reflection formula, i.e.
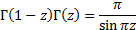
See also MnCGamma.
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Special Functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement