CornishFisher4
[this page | pdf | back links]
Function Description
Returns an array of 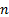 elements
containing the quantiles predicted by the 4th moment Cornish-Fisher asymptotic
expansion for a given input array of probability levels (with
elements
containing the quantiles predicted by the 4th moment Cornish-Fisher asymptotic
expansion for a given input array of probability levels (with 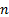 elements),
for a given mean, standard deviation, skew and (excess) kurtosis.
elements),
for a given mean, standard deviation, skew and (excess) kurtosis.
The Cornish-Fisher asymptotic expansion is a methodology for
predicting the shape of a (univariate) distributional form merely from the
moments of the distribution. The 4th moment variant uses the mean, standard
deviation, skew and (excess) kurtosis of the distribution.
For standardised returns (zero mean, unit standard
deviation), the 4th moment variant involves estimating the shape of the
quantile-quantile plot of the actual versus (standard) Normal distribution
using the following cubic equation, where 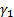 is
the skew and
is
the skew and 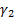 is
the (excess) kurtosis of the distribution:
is
the (excess) kurtosis of the distribution:
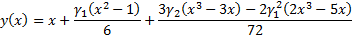
In the more generalised case where the mean, 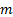 , is not
necessarily zero and the standard deviation,
, is not
necessarily zero and the standard deviation, 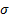 is not
necessarily unity the 4th moment variant involves estimating the shape of the
quantile-quantile plot as follows:
is not
necessarily unity the 4th moment variant involves estimating the shape of the
quantile-quantile plot as follows:
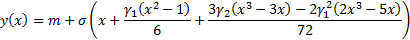
NAVIGATION LINKS
Contents | Prev | Next
Links to:
-
Interactively run function
-
Interactive instructions
-
Example calculation
-
Output type / Parameter details
-
Illustrative spreadsheet
-
Other Risk management functions
-
Computation units used
Note: If you use any Nematrian web service either programmatically or interactively then you will be deemed to have agreed to the Nematrian website License Agreement