Mixtures of normal distributions
[this page | pdf | references | back links]
1. Suppose we
have two Normal distributions, 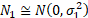 and
and 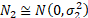 , with the same
mean (which without loss of generality is set to zero) but with different
standard deviations. Suppose that we form a mixture,
, with the same
mean (which without loss of generality is set to zero) but with different
standard deviations. Suppose that we form a mixture, 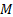 ,
of these two different distributions, i.e. a distribution where the probability
of drawing from the first distribution is
,
of these two different distributions, i.e. a distribution where the probability
of drawing from the first distribution is 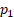 and from the
second distribution is
and from the
second distribution is 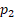 where
where 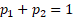 . The probability
density functions of the two distributions in isolation and of the mixture are:
. The probability
density functions of the two distributions in isolation and of the mixture are:
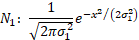
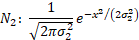
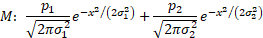
2. The
(excess) kurtosis of the mixture is as follows:
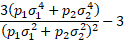
3. If 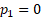 or
or 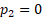 or
or 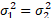 then the mixture
simplifies to a single normal distribution and thus has (excess) kurtosis of
zero. However in other situations the excess kurtosis is greater than zero.
This corresponds to the observation that the weighted arithmetic average of
different positive numbers is greater than their geometric average, as long as
more than one is given a positive weight.
then the mixture
simplifies to a single normal distribution and thus has (excess) kurtosis of
zero. However in other situations the excess kurtosis is greater than zero.
This corresponds to the observation that the weighted arithmetic average of
different positive numbers is greater than their geometric average, as long as
more than one is given a positive weight.
4. More
generally, if we have a mixture of several different normal distributions (e.g.
we postulate that we are in the presence of time-varying volatility and we are
measuring time averaged statistics), and if each of these normal distributions
has the same underlying mean, then we can expect our time averaged probability
distribution to appear to exhibit excess kurtosis.
5. If the
distributions have different means then the magnitude of the excess kurtosis
also depends on the means. In the above example, if 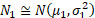 and
and 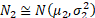 then the
probability density of the mixture becomes:
then the
probability density of the mixture becomes:
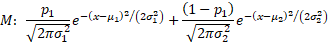
and its (excess) kurtosis becomes:
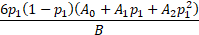
where
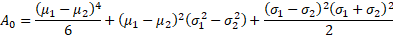
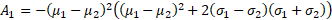
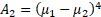
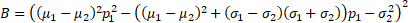
6. If the means are different enough (relative to
differences in the standard deviations then the excess kurtosis can be
negative, e.g. the excess kurtosis of an equal mixture (i.e. 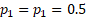 ) of
) of 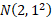 and
and 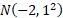 has an excess
kurtosis of
has an excess
kurtosis of 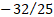 . This is
consistent with the observation that if the standard deviations of the every
component element of the mixture are arbitrarily small relative to the spread
of the means then any probability density function can be approximated
arbitrarily accurately by giving suitable weights to different elements of the
mixture, as long as there are enough suitably spaced contributors to the
mixture. The weight to give to the element with mean
. This is
consistent with the observation that if the standard deviations of the every
component element of the mixture are arbitrarily small relative to the spread
of the means then any probability density function can be approximated
arbitrarily accurately by giving suitable weights to different elements of the
mixture, as long as there are enough suitably spaced contributors to the
mixture. The weight to give to the element with mean 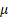 in
this formulation is the probability density at
in
this formulation is the probability density at 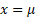 of
the desired overall probability distribution,
of
the desired overall probability distribution, 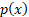 .
.