Marginal Value-at-Risk (Marginal VaR)
when underlying distribution is multivariate normal
[this page | pdf | back links]
Suppose we have a set of 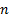 risk factors
which we can characterise by an
risk factors
which we can characterise by an 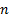 -dimensional
vector
-dimensional
vector 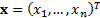 . Suppose that
the (active) exposures we have to these factors are characterised by another
. Suppose that
the (active) exposures we have to these factors are characterised by another 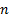 -dimensional
vector,
-dimensional
vector, 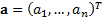 . Then the aggregate
exposure is
. Then the aggregate
exposure is 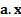 .
.
The Tail Value-at-Risk, 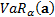 , of the
portfolio of exposures
, of the
portfolio of exposures 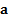 at confidence
level
at confidence
level 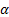 , is defined as
the value such that
, is defined as
the value such that 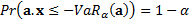 . The Marginal
Value-at-Risk,
. The Marginal
Value-at-Risk, 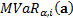 , is the
sensitivity of
, is the
sensitivity of 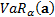 to a small change
in
to a small change
in 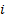 ’th exposure,
i.e.:
’th exposure,
i.e.:
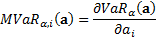
In the case where the risk factors are multivariate normally
distributed with mean 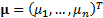 and covariance
matrix
and covariance
matrix 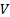 whose elements
are
whose elements
are 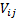 we have the
following.
we have the
following.
As 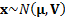 we have
we have 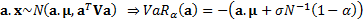 where
where 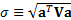 is the standard
deviation of the volatility of the (active) portfolio return, otherwise known
if we are focusing on active exposures as the (ex-ante) tracking error.
is the standard
deviation of the volatility of the (active) portfolio return, otherwise known
if we are focusing on active exposures as the (ex-ante) tracking error.
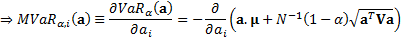
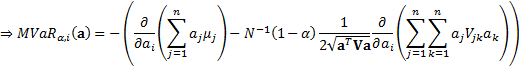
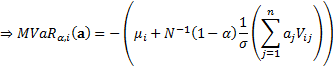
The last part of this equation can be expressed in terms of
the correlation between 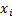 and
and 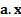 as follows.
Suppose we view the
as follows.
Suppose we view the 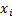 as corresponding
to time series
as corresponding
to time series 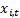 with
with 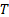 elements
(which without loss of generality can be assumed to be de-meaned, i.e. to have
their means set to zero) and
elements
(which without loss of generality can be assumed to be de-meaned, i.e. to have
their means set to zero) and 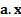 as corresponding
to a time series
as corresponding
to a time series 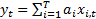 . Then the
correlation between
. Then the
correlation between 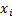 and
and 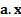 would be
(ignoring any small sample adjustment):
would be
(ignoring any small sample adjustment):
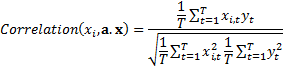
We would also have:
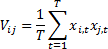
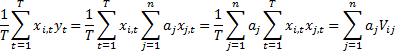
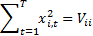
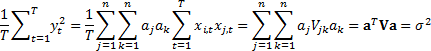
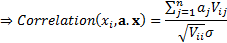
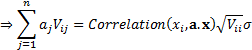
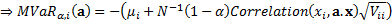
As risks arising from individual positions interact there is
no universally agreed way of subdividing the overall risk into contributions
from individual positions. However, a commonly used way is to define the Contribution
to Value-at-Risk, 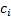 , of the
, of the 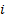 ’th
position,
’th
position, 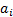 to be as
follows:
to be as
follows:
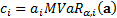
Conveniently the 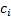 then sum to the
overall VaR:
then sum to the
overall VaR:
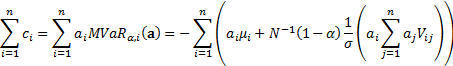
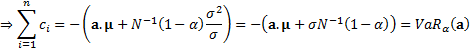
The property that the contributions to risk add to the total
risk is a generic feature of any risk measure that is (first-order)
homogeneous, a property that Value-at-Risk exhibits.