The Lanczos Approximation
[this page | pdf | back links]
The Lanczos approximation is a method for computing the gamma function numerically,
originally derived by Cornelius Lanczos in 1964 and involving the following
formula:
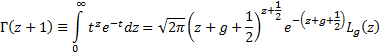
Here 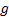 is an arbitrary constant
subject to the restriction that
is an arbitrary constant
subject to the restriction that 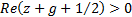 and
and 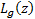 and
and
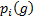 are
as follows, where
are
as follows, where 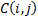 is
the
is
the 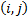 ’th
element of the Chebyshev polynomial coefficient matrix:
’th
element of the Chebyshev polynomial coefficient matrix:
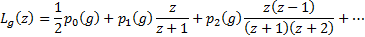
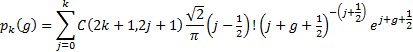
The series 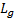 converges.
By choosing an appropriate
converges.
By choosing an appropriate 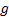 , typically a small
positive number, only a few terms are needed to calculate the gamma function to
a high degree of accuracy. The series approximation can then be recast into the
following form, with the
, typically a small
positive number, only a few terms are needed to calculate the gamma function to
a high degree of accuracy. The series approximation can then be recast into the
following form, with the 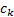 calculated
in advance:
calculated
in advance:
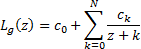
According to Wikipedia
(2015), Lanczos derived the formula by deriving the following integral
representation for the gamma function and then deriving a series expansion for
the integral within this representation: