Blending Independent Components and
Principal Components Analysis
2.7 Complexity pursuit
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
2.7 Complexity
pursuit
Most signals measured within a physical system can be
expected to be a mixture of statistically independent source signals. The most
parsimonious explanation for the complexity of an observed signal is thus that
it consists of a mixture of simpler signals, each from a different source.
Underpinning this is the assumption that a mixture of independent source
signals is typically more complex than the simplest (i.e. least complex) of its
constituent source signal. This complexity conjecture underpins the idea
of complexity pursuit.
One simple measure of complexity is predictability. If each
value of a signal is relatively easy to predict from previous signal values
then we might characterise the signal as having low complexity. Conversely, if
successive values of a signal are independent of each other then prediction is
in principle impossible and we might characterise such a signal as having a
high complexity.
Stone (2004), when discussing this technique, focuses on
minimising Kolmogorov complexity and defines a measure, 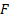 ,
of temporal predictability for a given set of signal mixtures
,
of temporal predictability for a given set of signal mixtures 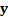 and weights,
and weights, 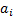 , applied to
these signal mixtures as follows:
, applied to
these signal mixtures as follows:
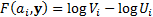
Here 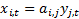 ,
, 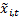 is a suitable
exponentially weighted moving average of
is a suitable
exponentially weighted moving average of 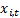 , i.e.
, i.e. 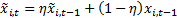 for some
suitable (perhaps predefined) value of
for some
suitable (perhaps predefined) value of 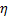 ,
, 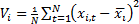 corresponds to
the overall variance of the given linear combination and
corresponds to
the overall variance of the given linear combination and 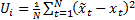 corresponds to
the extent to which it is well predicted by its previous values (assuming here
a first order autoregressive dependency).
corresponds to
the extent to which it is well predicted by its previous values (assuming here
a first order autoregressive dependency).
Complexity pursuit has certain advantages and disadvantages
over ICA and projection pursuit. Unlike ICA it does not appear explicitly to
include an a priori model for the signal pdfs, but seems only to depend on the
complexity of the signal. It ought therefore to be able to extract signals with
different pdf types. It also does not ignore signal structure, e.g. its
temporal nature if it is a time series. Conversely, ‘complexity’ is a less
obviously well-defined concept than independence or non-normality. For example,
the prescription introduced by Stone (2004)
and described above seems to be very heavily dependent on ‘lack of complexity’
being validly equated with signals exhibiting strong one-period autodependency.
NAVIGATION LINKS
Contents | Prev | Next