Blending Independent Components and
Principal Components Analysis
2.6 Infomax and maximum likelihood
independent components analysis
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
2.6 Infomax and
maximum likelihood independent components analysis
ICA as normally understood can be thought of as a
multivariate, parallel version of projection pursuit, i.e. an algorithm that
returns ‘all at once’ all of the unmixing weights applicable to all of the
input signals. Indeed, if ICA uses the same measure of ‘signal-likeness’ (i.e.
‘independence’, ‘non-normality’, ‘lack of complexity’) and assumes the same
number of signals exist as is used in the corresponding projection pursuit
methodology then the two should extract the same signals.
To the extent that the two differ, the core measure of
‘signal-likeness’ underlying most implementations of ICA is that of statistical
independence. As we have noted earlier, this is a stronger concept than mere
lack of correlation. To make use of this idea, we need a measure that tells us
how close to independent are any given set of unmixed signals.
Perhaps the most common measure used for this purpose is entropy.
This is often thought of as a measure of the uniformity of the distribution of
a bounded set of values. However, more generally, it can also be thought of as
the amount of ‘surprise’ associated with a given outcome. This requires some a
priori view of what probability distribution of outcomes is to be ‘expected’.
Surprise can then equated with relative entropy (i.e. Kullback-Leibler
divergence) which measures the similarity between two different probability
density functions.
The ICA approach thus requires an assumed probability
density function for the input signals and identifies the unmixing matrix that
maximises the joint entropy of the resulting unmixed signals. This is called
the infomax ICA approach. A common assumed probability density function (‘pdf’)
used for this purpose is a very high-kurtosis one such as some suitably scaled
version of 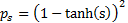 .
.
ICA can also be thought of as a maximum likelihood method
for estimating the optimal unmixing matrix. With maximum likelihood we again
need to specify an a priori probability distribution, in this case the assumed
joint pdf 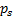 of the unknown
source signals, and we seek the unmixing matrix,
of the unknown
source signals, and we seek the unmixing matrix, 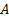 ,
that yields extracted signals
,
that yields extracted signals 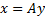 with a joint
pdf as similar as possible to
with a joint
pdf as similar as possible to 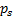 . In such
contexts, ‘as similar as possible’ is usually defined via the log likelihood
function, which results in the same answer as the equivalent infomax approach,
since both involve logarithmic functions of the underlying assumed probability
distribution.
. In such
contexts, ‘as similar as possible’ is usually defined via the log likelihood
function, which results in the same answer as the equivalent infomax approach,
since both involve logarithmic functions of the underlying assumed probability
distribution.
Both methods appear to rely on the frankly unrealistic
assumption that the model pdf is an exact match for the pdf of the source
signals. Of course, in general, the pdf of the source signals is not known
exactly. Despite this, ICA seems to work reasonably well. This is because we do
not really care about the form of the pdf. Indeed, it could correspond to a
quite extreme distribution. Instead all we really need for the approach to work
is for the model pdf to have the property that the closer any given
distribution is to it (in relative entropy or log likelihood terms), the more
likely that distribution is to correspond to a true source input signal. A
hyperbolic tangent (‘tanh’)-style pdf may be an unrealistic ‘model’ for a true
signal source, but use within the algorithm typically means that distributional
forms with high kurtosis will be preferentially selected versus ones with lower
kurtosis (even though neither may have a kurtosis anywhere near as large as
that exhibited by the hyperbolic tangent pdf itself). It is the relative ordering
of distributional forms introduced by choice of model pdf that is important
rather than the structure of the model pdf per se. As a tanh-style model pdf
preferentially extracts signals exhibiting high kurtosis it will extract
similar signals to those extracted by kurtosis-based projection pursuit
methods. Indeed, it ought to be possible to select model pdfs (or at least
definitions of how to order likenesses of distributional forms to the model
pdfs) that exactly match whatever metric is used in a corresponding projection
pursuit methodology (even if this isn’t how the ICA methodology was originally
developed).
To estimate the unmixing matrix 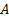 (
(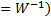 that maximises
the relative entropy or log likelihood and hence corresponds to the supposed
input signals, we could again use brute force. However, again it is more
efficient to use some sort of gradient ascent method as per Section
2.8, iteratively adjusting the estimated
that maximises
the relative entropy or log likelihood and hence corresponds to the supposed
input signals, we could again use brute force. However, again it is more
efficient to use some sort of gradient ascent method as per Section
2.8, iteratively adjusting the estimated 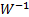 in order to
maximise the chosen metric.
in order to
maximise the chosen metric.
NAVIGATION LINKS
Contents | Prev | Next