Blending Independent Components and
Principal Components Analysis
2.4 Signal Mixtures
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
2.4 Signal Mixtures
As noted earlier, ICA typically assumes that outputs are
(linear combination) mixtures of inputs, i.e. are derived by adding
together input signals in fixed proportions. If there are 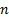 input
(i.e. source) signals then there need to be at least
input
(i.e. source) signals then there need to be at least 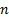 different
mixtures for us to be able to differentiate between the sources. In practice,
the number of signal mixtures is often larger than the number of source
signals. For example, with electroencephalography (EEG), the number of signal
mixtures is equal to the number of electrodes placed on the head (typically at
least 10) but there are typically fewer sources than this. If the number of
signals is known to be less than the number of signal mixes then the number of
signals extracted by ICA can be reduced by dimension reduction, either by
preprocessing the signal mixtures, e.g. by using PCA techniques, or by
arranging for the ICA algorithm to return only a specified number of signals.
different
mixtures for us to be able to differentiate between the sources. In practice,
the number of signal mixtures is often larger than the number of source
signals. For example, with electroencephalography (EEG), the number of signal
mixtures is equal to the number of electrodes placed on the head (typically at
least 10) but there are typically fewer sources than this. If the number of
signals is known to be less than the number of signal mixes then the number of
signals extracted by ICA can be reduced by dimension reduction, either by
preprocessing the signal mixtures, e.g. by using PCA techniques, or by
arranging for the ICA algorithm to return only a specified number of signals.
Such mixtures can be expressed succinctly in matrix form, 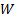 ,
where the coefficients of
,
where the coefficients of 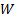 are the
are the 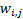 referred to
above. We can then write the formula deriving the output signals from the input
signals as:
referred to
above. We can then write the formula deriving the output signals from the input
signals as:
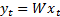
We note that we have implicitly assumed a model of the world
involving time homogeneity (or spatial homogeneity, if the
signals involve a spatial dimension rather than a time dimension) i.e. that the
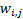 and hence
and hence 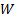 are
constant through time.
are
constant through time.
If the mixing coefficients, i.e. the elements of 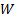 ,
are known already then we can typically easily derive the input signals from
the output matrix by inverting this matrix equation, i.e.
,
are known already then we can typically easily derive the input signals from
the output matrix by inverting this matrix equation, i.e. 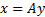 where
where
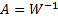 .
.
However, we are more usually interested in the situation
where the mixing coefficients are unknown (although as we have stated,
we do implicitly assume with ICA that the mixture can be expressed in the above
form, and that the corresponding coefficients are constant through time). We
therefore seek an algorithm that estimates the unmixing coefficients, i.e. the
coefficients 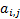 of
of 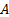 ,
directly from the data, allowing us then to recover the signals themselves (and
the original mixing coefficients).
,
directly from the data, allowing us then to recover the signals themselves (and
the original mixing coefficients).
We note that there is no way in such a framework of
distinguishing between two input signals that are constant multiples of each
other. Thus ICA and its variants will only generally identify signals up to a
scalar multiplier (although we might in practice impose some standardised
scaling criteria when presenting the answers or deciding which signals to
retain and which to discard as ‘insignificant’ or unlikely to correspond to a
true input signal).
If the number of input and output signals is the same then a
matrix such as 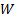 can be viewed
as corresponding to a vector transformation in an
can be viewed
as corresponding to a vector transformation in an 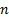 -dimensional
vector space (
-dimensional
vector space (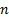 being the
number of input signals) spanned by vectors corresponding to the input signals.
In this representation, each input signal would be characterised by a vector of
unit length in the direction of a particular axis in this
being the
number of input signals) spanned by vectors corresponding to the input signals.
In this representation, each input signal would be characterised by a vector of
unit length in the direction of a particular axis in this 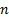 -dimensional
space, with each different pair of input signals being orthogonal to
each other (in geometric terms, ‘perpendicular’ to each other). Any possible
(linear combination) mixture of these signals then corresponds to some vector
in the same vector space, and a set of
-dimensional
space, with each different pair of input signals being orthogonal to
each other (in geometric terms, ‘perpendicular’ to each other). Any possible
(linear combination) mixture of these signals then corresponds to some vector
in the same vector space, and a set of 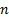 of them
corresponds to a set of
of them
corresponds to a set of 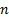 vectors in
such a space. An
vectors in
such a space. An 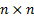 matrix thus
defines how simultaneously to map one set of
matrix thus
defines how simultaneously to map one set of 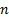 vectors
to another in a way that respects underlying linear combinations. The types of
transformations that are catered for by such matrices include rotation,
shearing, and expansion away from or contraction towards the origin. Inverting
such a matrix (if this is possible) corresponds to identifying the
corresponding inverse transformation that returns a set of
vectors
to another in a way that respects underlying linear combinations. The types of
transformations that are catered for by such matrices include rotation,
shearing, and expansion away from or contraction towards the origin. Inverting
such a matrix (if this is possible) corresponds to identifying the
corresponding inverse transformation that returns a set of 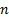 transformed
signal vectors to their original positions.
transformed
signal vectors to their original positions.
ICA uses this insight by identifying which (orthogonal)
mixtures of the output series seem to exhibit the largest amount of
‘independence’, ‘non-normality’ or ‘lack of randomness’, since these mixtures
can then be expected to correspond to the original input series (or scalar
multiples of them). We note that not only will ICA not be able to differentiate
between two signals that are scalar multiples of each other, but also that it
won’t be able to differentiate between, say, two different pairs of signals in
which the ordering of the signals is reversed. This is because it doesn’t
directly include any prescription that ensures that any particular input signal
will be mapped back to its own original axis. Instead, it is merely expected to
arrange for each input signal to be mapped back to any one of the original
(orthogonal) axes (but for no two different input signals to be mapped back
onto the same axis). However, there may be a natural ordering that can be
applied to the extracted signals, e.g. if input signals are expected to be
strongly non-normal then we might order the extracted signals so that the first
one is the most non-normal according to the relevant measure of non-normality
that we have chosen, etc.
NAVIGATION LINKS
Contents | Prev | Next