Blending Independent Components and
Principal Components Analysis
2.2 Linear combination versus
distribution mixtures
[this page | pdf | references | back links]
Return to
Abstract and Contents
Next page
2.2 Linear combination
versus distribution mixtures
Typically ICA assumes that the observed signals are a
specific type of mixture of the underlying factors, namely a linear
combination of these factors. The mixing coefficients applicable to
this sort of mixture are the multipliers applied to each factor in the
computation of the relevant output signal.
It is worth noting that the term ‘mixture’ has a variety of
meanings in statistics. Here it is being used to mean that the output signals, 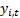 , are derived
from the input signals,
, are derived
from the input signals, 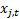 using the
following formula (where
using the
following formula (where 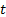 indexes the
observed values of a given signal, and so might correspond to points in time or
space, and
indexes the
observed values of a given signal, and so might correspond to points in time or
space, and 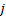 indexes the
signals themselves):
indexes the
signals themselves):
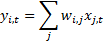
The term ‘mixture’ can also be used to describe a
probability distribution for a random variable that is sequentially drawn with
given probabilities from one of a number of different underlying distributions.
The ‘mixing coefficients’ for such distribution mixtures relate to the
probability of the given draw coming from the relevant underlying probability
distribution. Such distribution mixtures can behave quite differently to the
sorts of linear combination mixtures described above. We will explore the relevance
of this latter type of mixture to portfolio risk management in Section
4.3.
NAVIGATION LINKS
Contents | Prev | Next