Extreme Events – Specimen Question
A.5.2(a) – Answer/Hints
[this page | pdf | references | back links]
Return
to Question
Q. You know that she has also
used mean-variance optimisation techniques and adopted the same expected
covariances as you would have done in A.5.1. What return assumptions might she
have adopted when choosing her portfolio mix? Specify mathematically all possible
sets of return assumptions she could have adopted and still reached this
answer.
The return assumptions that your colleague might have used
can be derived using implied alphas. These are the (mean) returns that your
colleague needs to have assumed will apply for the portfolio in question to be
deemed efficient.
No constraints are biting in relation to the specific
portfolio mix in question (apart from the constraint that all weights add to
unity). If returns assumed for each asset category are characterised by the
vector 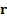 and if
the portfolio weights are characterised by the vector
and if
the portfolio weights are characterised by the vector 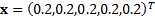 then we
need
then we
need 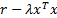 to be at
a maximum, subject to the constraint that
to be at
a maximum, subject to the constraint that 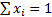 . Using
Lagrange multipliers as per Section 5.10 of Extreme Events, this
implies that:
. Using
Lagrange multipliers as per Section 5.10 of Extreme Events, this
implies that:
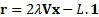
It is relatively straightforward to calculate an example  that
satisfies this equation using Microsoft Excel. Alternatively, you could use the
Nematrian web function, MnReverseQuadraticPortfolioOptimiser,
which assumes
that
satisfies this equation using Microsoft Excel. Alternatively, you could use the
Nematrian web function, MnReverseQuadraticPortfolioOptimiser,
which assumes 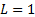 but
allows an arbitrary choice of
but
allows an arbitrary choice of 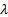 (the
input parameter is there called the ‘TradeOffFactor’). Choosing
(the
input parameter is there called the ‘TradeOffFactor’). Choosing 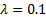 gives
the following possible values for
gives
the following possible values for 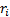 :
:
|
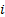
|
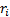
|
|
1 (i.e. A1)
|
-0.288
|
|
2 (i.e. A2)
|
-0.864
|
|
3 (i.e. A3)
|
2.656
|
|
4 (i.e. A4)
|
5.18
|
|
5 (i.e. A5)
|
6.48
|
NAVIGATION LINKS
Contents | Prev | Next | Question