Extreme Events – Specimen Question
A.4.2(a) – Answer/Hints
[this page | pdf | references | back links]
Return
to Question
Q. Identify the series
corresponding to the principal components of Indices A and B
There are several different ways of identifying the series
corresponding to the principal components of A and B.
The first point to note is that these series are only
computable up to a mean drift term and up to a scalar multiple, although it is
conventional to arrange for the series to have zero mean and for them to be
scaled in magnitude according to some suitable convention.
Thus, it is easiest to work with the following adjusted
data, which involve application of constant adjustments to the original data so
that they now have zero means:
|
Period
|
Adjusted logged return A (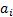 , say) , say)
|
Adjusted logged return B (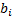 , say) , say)
|
|
1
|
-0.2856959
|
0.0511585
|
|
2
|
0.0043199
|
-0.1719851
|
|
3
|
0.2200434
|
-0.1231949
|
|
4
|
0.0793551
|
-0.0280909
|
|
5
|
-0.0107785
|
-0.0952445
|
|
6
|
0.0083080
|
0.0013678
|
|
7
|
-0.0026977
|
-0.0777577
|
|
8
|
0.0132707
|
0.0299835
|
|
9
|
0.0737789
|
0.1254705
|
|
10
|
-0.1245130
|
0.0172569
|
|
11
|
0.0102960
|
-0.1085632
|
|
12
|
0.0112886
|
0.1130148
|
|
13
|
-0.0354204
|
0.1670349
|
|
14
|
0.0309356
|
0.0949475
|
|
15
|
-0.0406315
|
0.0821033
|
|
16
|
-0.0087522
|
-0.0627037
|
|
17
|
-0.0692503
|
-0.0788417
|
|
18
|
0.0662952
|
-0.0209003
|
|
19
|
0.0386876
|
0.0549608
|
|
20
|
0.0211603
|
0.0299835
|
The first principal component can be found by finding the 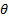 (
(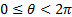 )
which maximises the standard deviation of
)
which maximises the standard deviation of 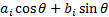 . The
weights to give to A and B in constructing the principal
component series are then
. The
weights to give to A and B in constructing the principal
component series are then 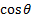 and
and 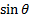 respectively.
Subsequent principal components can be found by Gram-Schmidt orthogonalisation.
This is possible to do in Microsoft Excel, e.g. using the Solver Add-in, but is
rather convoluted. With this data the
respectively.
Subsequent principal components can be found by Gram-Schmidt orthogonalisation.
This is possible to do in Microsoft Excel, e.g. using the Solver Add-in, but is
rather convoluted. With this data the 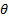 (in
radians) corresponding to the first principal component is -0.7136 and
that for the second (i.e. in this case, other) principal component is 0.8572
(in
radians) corresponding to the first principal component is -0.7136 and
that for the second (i.e. in this case, other) principal component is 0.8572
Simpler is to use a standard statistics package that
identifies the principal component weights directly from the underlying data or
to use the corresponding web service function available via the Nematrian
website, i.e. MnPrincipalComponentsWeights
which using this data returns an array:
|
Principal Component
|
Multiplier to apply to 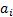
|
Multiplier to apply to 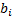
|
|
1
|
0.756
|
-0.655
|
|
2
|
0.655
|
0.756
|
The Nematrian website also provides a web service function
which calculates the principal component series directly, i.e. applies these
weights to the underlying (adjusted) data series. This is MnPrincipalComponents.
NAVIGATION LINKS
Contents | Prev | Next | Question