Elliptical distributions
[this page | pdf | back links]
An elliptical distribution is a multivariate distribution
whose (multivariate) characteristic function, 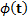 ,
, 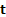 being a vector with
the same number of entries as there are dimensions for the distribution, of the
form:
being a vector with
the same number of entries as there are dimensions for the distribution, of the
form:
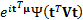
where 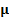 is a specified
variable, and
is a specified
variable, and 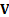 is a positive definite
matrix.
is a positive definite
matrix.
If the distribution has a probability density function then
it will take the form:
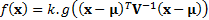
where 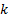 is a scale factor,
is a scale factor, 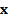 is an n-dimensional
random vector with median vector
is an n-dimensional
random vector with median vector 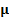 (which is also the
mean vector, if the latter exists), is a positive definite matrix which is
proportional to the covariance matrix if the latter exists, and
(which is also the
mean vector, if the latter exists), is a positive definite matrix which is
proportional to the covariance matrix if the latter exists, and 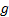 is a
function mapping non-negative real numbers to non-negative real numbers with
finite area under the curve.
is a
function mapping non-negative real numbers to non-negative real numbers with
finite area under the curve.
Perhaps the best known elliptical distributions are
multivariate normal (i.e. Gaussian) distributions.