Showing that VaR is not coherent for
exponentially distributed loss variables
[this page | pdf | back links]
Please bear in mind that in general a multivariate
distribution each of the marginal of which is exponentially distributed is not
necessarily a member of the exponential family of (multivariate) distributions.
The simplest case to consider is where two loss variables
come from the same exponential
distribution with parameter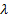 
.
The probability density function of 
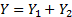where
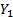and
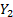are
independent random variables each coming from an exponential distribution with
parameter 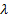is
.
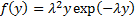The VaR
at confidence level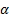 
for
,
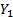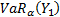is
the same as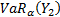 
and
is the value of 
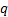for
which:
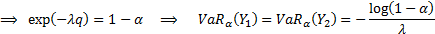
The VaR at the same confidence level for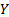 
is
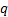the value of for
which
Integrating by parts we have:
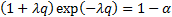
The exponential distribution (with independent variables) is
not elliptical so VaR’s for it shouldn’t be coherent. More specifically it
should be possible to identify a suitable 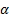for
which VaR is not sub-additive, i.e. for which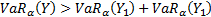 
,
as sub-additivity is one of the axioms required for coherence.
Although there is no certainty that this is the case it is likely that such a
situation will arise either where 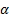is
close to zero or when is
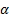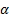close to 1. The case where is
close to 1 does not look promising as the behaviour of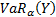 
will
tend to be dominated by the exponential term. So instead let us consider the
case where when 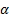is
close to 0. We then have for :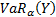
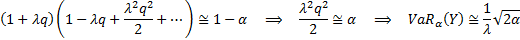
However in these circumstances:
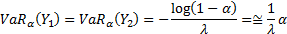
So if 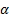is
small enough we will have 
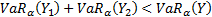as
desired to prove the conjecture.