Estimating operational risk capital
requirements assuming data follows a bi-uniform or a triangular distribution
(using maximum likelihood)
[this page | pdf | back links]
Suppose a risk manager believes that an appropriate model
for a particular type of operational risk exposure involves the loss, 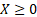 ,
never exceeding an upper limit,
,
never exceeding an upper limit, 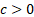 ,
and the probability density function
,
and the probability density function 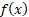 taking
the form of a bi-uniform distribution:
taking
the form of a bi-uniform distribution:
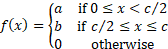
where 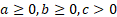 are
all constant.
are
all constant.
Suppose we want to estimate maximum likelihood estimators
for 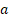 ,
,
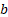 and
and
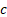 given
losses of
given
losses of 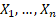 ,
say and hence to estimate a Value-at-Risk for a given confidence level for this
loss type, assuming that the probability distribution has the form set out
above.
,
say and hence to estimate a Value-at-Risk for a given confidence level for this
loss type, assuming that the probability distribution has the form set out
above.
We note that 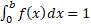 for
for
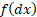 to
correspond to a probability density function, so:
to
correspond to a probability density function, so:
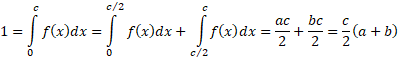
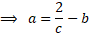
Suppose the 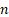 losses,
losses,
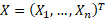 ,
are assumed to be independent draws from a distribution with probability
density function
,
are assumed to be independent draws from a distribution with probability
density function 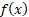 and
suppose
and
suppose 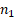 of
these losses are less
of
these losses are less 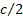 and
and
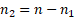 are
greater than
are
greater than 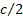 .
The likelihood is then:
.
The likelihood is then:
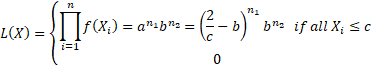
This will be maximised for some value that has 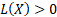 ,
i.e. has
,
i.e. has 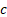 at
least as large as
at
least as large as 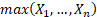 .
In such circumstances the likelihood is maximised when the log likelihood is
maximised which will be when
.
In such circumstances the likelihood is maximised when the log likelihood is
maximised which will be when 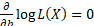 ,
i.e. when
,
i.e. when 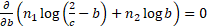 ,
i.e. when:
,
i.e. when:
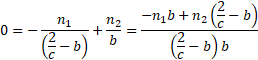
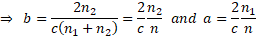
(assuming 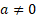 and
and
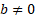 )
)
For these values of 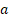 and
and
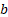 the
log likelihood is then:
the
log likelihood is then:
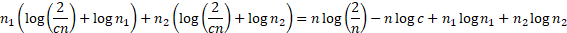
In most circumstances this will be maximised when 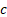 is
as small as possible, provided
is
as small as possible, provided 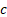 is
still at least as large as
is
still at least as large as 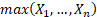 so
the maximum likelihood estimators are:
so
the maximum likelihood estimators are:
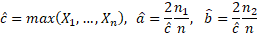
However, it is occasionally necessary to consider the case
where we select a 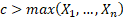 and
have
and
have 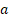 and/or
and/or
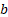 equal
to zero.
equal
to zero.
To estimate a VaR at a confidence level 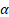 we
need to find the value
we
need to find the value 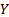 for
which the loss is expected to exceed
for
which the loss is expected to exceed 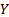 only
only
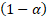 %
of the time, i.e.
%
of the time, i.e. 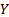 such
that (if
such
that (if 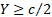 ):
):
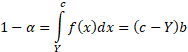
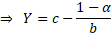
A similar approach can be used for tri-uniform distributions
or other more complex piecewise uniform distributions.
Somewhat more complex is if 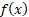 takes
the form of a triangular distribution, i.e. where:
takes
the form of a triangular distribution, i.e. where:
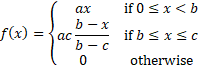
where 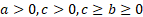 are
all constant.
are
all constant.
Nguyen
and McLachlan (2016), when developing a new algorithm for maximum
likelihood estimation of triangular or more general polygonal distributions,
note that in the case where 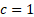 and
and
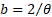 then
Oliver (1972), “A maximum likelihood oddity”, American Statistician 26, 43–44, indicates
that
then
Oliver (1972), “A maximum likelihood oddity”, American Statistician 26, 43–44, indicates
that 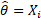 for
some
for
some 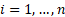 and
moreover that if the sample is ordered so that
and
moreover that if the sample is ordered so that 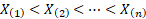 then
then
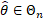 where:
where:
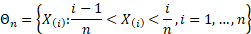
Asymptotically, on average, the number of observations in 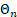 appears
to be approximately two.
appears
to be approximately two.
We can apply this reasoning to the more general triangular
distribution where we do not know 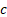 by
again noting that in many cases the log-likelihood will be minimised by setting
by
again noting that in many cases the log-likelihood will be minimised by setting
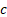 to
be as small as possible, provided
to
be as small as possible, provided 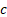 is
still at least as large as
is
still at least as large as 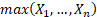 ,
and then separately handling cases where the likelihood can be improved by
selecting a higher value for
,
and then separately handling cases where the likelihood can be improved by
selecting a higher value for 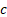 .
.