Estimating operational risk capital
requirements assuming data follows a gamma distribution (using the method of
moments)
[this page | pdf | back links]
Suppose a firm has collated past operational annual loss
data and the distribution of these annual losses is expected to provide a good
guide to the distribution of future annual losses. Suppose the annual losses
are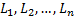 
.
Suppose also that the losses come from a gamma distribution with probability
density function:
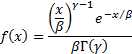
where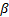 
is
a scale parameter (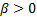
)
and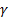 
is
a shape parameter (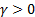
).
One way of estimating 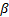and
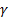is
to use the ‘method of moments’ which for the gamma distribution can be done
analytically.
We note that the gamma function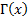 
is
defined as:
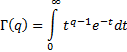
This means that it has the property that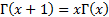 
for
.
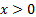It also means (for 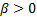and
)
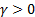that the following is true (which is necessary for the probability density of
the gamma distribution to integrate to unity):
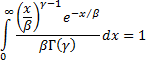
We next note that the gamma distribution has the property
that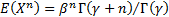 
.
This is because:
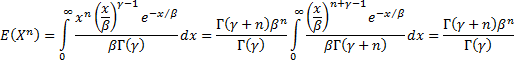
To use the method of moments we will calculate the first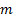 
moments
of the observed data where 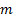is
the number of parameters to estimate. The gamma distribution has two parameters
so here we have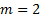 
and
in this instance we calculate the first two moments (or equivalently the mean
and variance) of the observed data and also the same two moments if the data
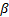comes from a gamma distribution with parameters and
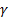respectively.
We then select values of 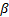and
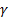that
simultaneously equate the observed moments with the distributional moments.
For the gamma distribution we have:
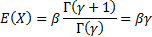
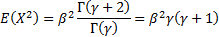
So the mean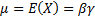 
and
the variance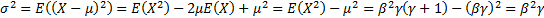 
.
The observed (sample) mean and variance [note it is not
absolutely clear with method of moments whether to use the sample or population variance]
are:
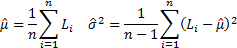
So, with the method of moments we would select 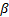and
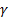so
that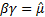 
,
,
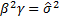i.e. 
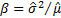and
.
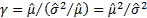If more recent observations were believed to be more
relevant than less recent observations then we could give greater weight to
more recent observations in the calculation of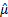 
and
,
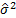e.g. if the weights were 
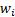then
we might use (if we were focusing on population moments):
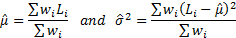
[N.B. See here for
insights on how to calculate weighted sample moments]
Another common method of estimating parameter values is to
use maximum likelihood estimation, which cannot in general be done analytically
for the gamma distribution but can be done numerically using e.g. the Nematrian
website function MnProbDistMLE.
Of course, to estimate, say, a Value-at-Risk for
operational risk you would ideally not just rely on past annual operational
loss data. Additional information you might seek (and why you might seek it)
includes:
From within the firm
Ideally, it would be helpful to have individual losses (so
that you have amounts and frequency) allowing you to analyse loss size, i.e.
severity, and loss frequency separately. Also desirable would be losses
subdivided into appropriate categories, as this should provide extra colour on
the losses being suffered. It would ideally also be helpful to have ‘volume’ statistics
that are believed to be correlated with loss frequency. For example,
operational losses might be expected to be linked to number of customers, staff
turnover, funds under management etc. This sort of volume data should help you
to estimate future annual losses better and also to get a better understanding
of past behaviour.
From elsewhere
Hopefully the firm’s historic operational losses have been
relatively small and have also been infrequent. Its own historical data may not
therefore provide a good guide to the magnitude of large losses it might incur
in the future. Access to other firms’ experience, including e.g. data collected
by industry bodies, is therefore likely to be helpful, as long as the
industry-wide experience is expected to be relevant to the firm.