Estimating operational risk capital
requirements assuming data follows a bi-exponential distribution
[this page | pdf | back links]
Suppose a risk manager believes that an appropriate model
for a particular type of operational risk exposure involves the loss, 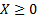 ,
coming 50% of the time from an exponential
distribution with parameter
,
coming 50% of the time from an exponential
distribution with parameter 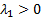 and
50% of the time come from an exponential distribution with parameter
and
50% of the time come from an exponential distribution with parameter 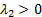 .
The exponential distribution
.
The exponential distribution 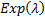 has
a probability density function,
has
a probability density function, 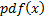 ,
mean,
,
mean, 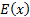 ,
and variance
,
and variance 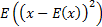 as
follows:
as
follows:
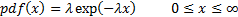
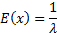
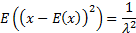
Suppose we want method of moments (MoM) estimators for 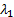 and
and
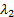 and
we have loss data
and
we have loss data 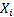 for
for
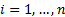 where
the number of losses,
where
the number of losses, 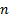 ,
is sufficiently large to be able to ignore small sample corrections. Then the
MoM estimators can be derived as follows, where the (sample) moments used in
the estimation are
,
is sufficiently large to be able to ignore small sample corrections. Then the
MoM estimators can be derived as follows, where the (sample) moments used in
the estimation are 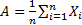 and
and
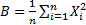 .
.
The pdfs of the individual parts, 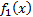
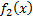 ,
and of the overall distribution,
,
and of the overall distribution, 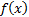 ,
are:
,
are:

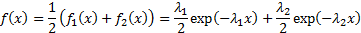
The mean of 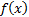 is:
is:
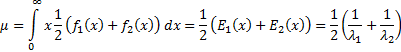
where 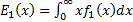 and
and
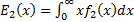
By integrating by parts or by noting that 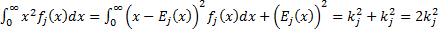 for
for
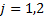 where
where 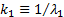 and
and
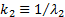 ,
we note that
,
we note that
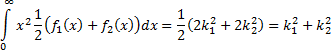
So method of moments estimators involve (if these
simultaneous equations have a (real) solution):
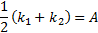
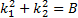
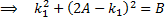
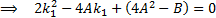
This is a quadratic equation which has the following
solutions:
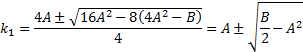
The two roots correspond to 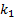 and
and
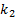 (it
is not possible to differentiate between them given merely the data being
provided). Hence the values of
(it
is not possible to differentiate between them given merely the data being
provided). Hence the values of 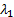 and
and
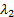 are:
are:
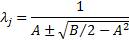
In practice it is more likely that the probabilities of
drawing from the underlying exponentials are unknown. This adds an extra degree
of freedom which would introduce the need to include a further (higher) moment
into the parameter estimation process.